题目内容
11．
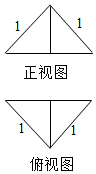把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥A-BCD的正视图和俯视图如图所示，则其几何体的表面积为（ ）| A． | $\frac{2+\sqrt{2}}{2}$ | B． | $\frac{2+\sqrt{3}}{2}$ | C． | 1+$\sqrt{2}$ | D． | 1+$\sqrt{3}$ |
分析 由主视图可知三棱锥侧面ABD与底面BCD垂直，求出棱锥的高即可得出另2个侧面为等边三角形，从而可求出几何体的表面积．
解答 
解：由主视图的腰长为1可知侧面ABD⊥底面BCD，
取BD的中点O，则AO=OC=$\frac{\sqrt{2}}{2}$，∴AC=$\sqrt{2}$AO=1，
∴△ABC，△ACD是等边三角形，
∴几何体的表面积为为$\frac{1}{2}+\frac{1}{2}+\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}$=$\frac{2+\sqrt{3}}{2}$．
故选B．
点评 本题考查了棱锥的三视图，结构特征与表面积计算，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．如图是一个四面体的三视图，则该四面体的体积为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{3}{8}$ |
16．
如图，网络纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的表面积为（
如图，网络纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的表面积为（| A． | 17π | B． | 22π | C． | 68π | D． | 88π |
3．函数f（x）=sin（$\frac{π}{3}$-2x）的单调递增区间是（ ）
| A． | [-kπ-$\frac{π}{12}$，-kπ+$\frac{5π}{12}$]，k∈Z | B． | [2kπ-$\frac{π}{6}$，2kπ+$\frac{5π}{6}$]，k∈Z | ||
| C． | [kπ+$\frac{5π}{12}$，kπ+$\frac{11π}{12}$]，k∈Z | D． | [kπ-$\frac{π}{6}$，kπ+$\frac{π}{3}$]，k∈Z |