题目内容
2．如图是一个四面体的三视图，则该四面体的体积为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{3}{8}$ |
分析 由已知三视图得到几何体为棱长为2的正方体切去部分后得到四面体，计算四面体的体积．
解答 
解：由已知三视图得到几何体如图四面体A-BCD，是由棱长为2 的正方体切割得到，其中AE=2$\sqrt{2}$，CD=$\sqrt{2}$，梯形ADCE的面积为$\frac{1}{2}×（\sqrt{2}+2\sqrt{2}）×\frac{3\sqrt{2}}{2}$，B到梯形ADCE的距离为$\frac{1}{3}$，
所以四面体的体积为$\frac{1}{3}$VB-ADCE
=$\frac{1}{3}×\frac{1}{3}×（\sqrt{2}+2\sqrt{2}）×\frac{3\sqrt{2}}{2}×\frac{1}{2}×\frac{1}{3}=\frac{1}{6}$；
故选C．
点评 本题考查了由几何体的三视图求体积；关键是由三视图正确还原几何体．
练习册系列答案
相关题目
8．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的一条渐近线方程为y=$\frac{{\sqrt{5}}}{2}$x，且与椭圆$\frac{x^2}{12}+\frac{y^2}{3}$=1有公共焦点，则C的方程为（ ）
| A． | $\frac{x^2}{8}-\frac{y^2}{10}=1$ | B． | $\frac{x^2}{5}-\frac{y^2}{4}=1$ | C． | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | D． | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
10．已知函数f（x）=loga（1-ax）（a＞0，a≠1），则不等式f（x）＞f-1（1）的解为（ ）
| A． | （-1，0） | B． | （0，1] | C． | （0，1） | D． | （1，+∞） |
17．
如图，某几何体的三视图中，俯视图是边长为2的正三角形，正视图和左视图分别为直角梯形和直角三角形，则该几何体的体积为（ ）
如图，某几何体的三视图中，俯视图是边长为2的正三角形，正视图和左视图分别为直角梯形和直角三角形，则该几何体的体积为（ ）| A． | $\frac{{3\sqrt{3}}}{2}$ | B． | $3\sqrt{3}$ | C． | $\frac{{9\sqrt{3}}}{2}$ | D． | $\frac{{3\sqrt{3}}}{4}$ |
11．
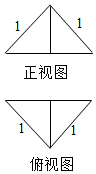把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥A-BCD的正视图和俯视图如图所示，则其几何体的表面积为（ ）
把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥A-BCD的正视图和俯视图如图所示，则其几何体的表面积为（ ）| A． | $\frac{2+\sqrt{2}}{2}$ | B． | $\frac{2+\sqrt{3}}{2}$ | C． | 1+$\sqrt{2}$ | D． | 1+$\sqrt{3}$ |