题目内容
3.函数f(x)=sin($\frac{π}{3}$-2x)的单调递增区间是( )| A. | [-kπ-$\frac{π}{12}$,-kπ+$\frac{5π}{12}$],k∈Z | B. | [2kπ-$\frac{π}{6}$,2kπ+$\frac{5π}{6}$],k∈Z | ||
| C. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | D. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z |
分析 利用诱导公式化简函数的解析式,再利用正弦函数的单调性,求得该函数的增区间.
解答 解:函数f(x)=sin($\frac{π}{3}$-2x)=-sin(2x-$\frac{π}{3}$),令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,
求得kπ+$\frac{5π}{12}$≤x≤kπ+$\frac{11π}{12}$,可得函数f(x)的增区间为[得kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z,
故选:C.
点评 本题主要考查诱导公式、正弦函数的单调性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线方程为y=$\frac{{\sqrt{5}}}{2}$x,且与椭圆$\frac{x^2}{12}+\frac{y^2}{3}$=1有公共焦点,则C的方程为( )
| A. | $\frac{x^2}{8}-\frac{y^2}{10}=1$ | B. | $\frac{x^2}{5}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
11.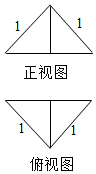 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )
 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )| A. | $\frac{2+\sqrt{2}}{2}$ | B. | $\frac{2+\sqrt{3}}{2}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
15.若双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线过点(2,$\sqrt{21}$),则此双曲线的离心率为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | $\frac{\sqrt{13}}{2}$ |
13.若X~B(n,$\frac{1}{3}$),且D(X)=$\frac{2}{3}$,则P(0≤X≤2)等于( )
| A. | $\frac{1}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{26}{27}$ | D. | $\frac{1}{27}$ |