题目内容
16.曲线f(x)=2x2+x-2在P0处的切线平行于直线y=5x-1,则点P0坐标为(1,1).分析 设出切点坐标,求出函数在切点处的导数值,利用切线平行于直线y=5x-1得到切点处的导数值是5,求出切点横坐标,代入曲线f(x)=2x2+x-2求得切点纵坐标.
解答 解:设P0(x0,y0),
由f(x)=2x2+x-2,得f′(x)=4x+1,
∴f′(x0)=4x0+1,
∵曲线f(x)在点P0处的切线平行于直线y=5x-1,
∴4x0+1=5,解得:x0=1.
当x0=1时,y0=2×12+1-2=1;
∴点P0坐标为(1,1).
故答案为:(1,1).
点评 本题考查利用导数研究曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是该点处的导数值,考查了两直线平行与斜率之间的关系,是中档题.

练习册系列答案
相关题目
6.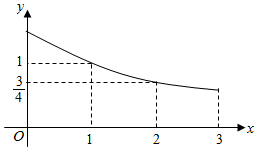 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )| A. | [-2,1] | B. | [-3,-2]∪(0,3] | C. | [-2,0]∪(1,4] | D. | [-3,0]∪[2,5] |
1.已知集合M={ x|x≥-$\frac{1}{2}$},N={x|1-x2≥0},则M∪N=( )
| A. | [-$\frac{1}{2}$,1] | B. | [-1,1] | C. | (-1,+∞) | D. | [-1,+∞) |
8.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线方程为y=$\frac{{\sqrt{5}}}{2}$x,且与椭圆$\frac{x^2}{12}+\frac{y^2}{3}$=1有公共焦点,则C的方程为( )
| A. | $\frac{x^2}{8}-\frac{y^2}{10}=1$ | B. | $\frac{x^2}{5}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
10.已知函数f(x)=loga(1-ax)(a>0,a≠1),则不等式f(x)>f-1(1)的解为( )
| A. | (-1,0) | B. | (0,1] | C. | (0,1) | D. | (1,+∞) |
11.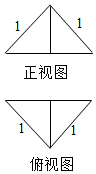 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )
 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )| A. | $\frac{2+\sqrt{2}}{2}$ | B. | $\frac{2+\sqrt{3}}{2}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |