题目内容
1.如果对定义在区间D上的函数f(x),对区间D内任意两个不相等的实数x1,x2,都有x1f(x1)+x2f(x2)>x${\;}_{{\;}_{1}}$f(x2)+x2f(x1),则称函数f(x)为区间D上的“H函数”,给出下列函数及函数对应的区间①y=$\frac{1}{3}$x3-$\frac{1}{2}$x2+$\frac{1}{2}$x,(x∈R)
②y=3x+cosx-sinx,x∈(0,$\frac{π}{2}$)
③f(x)=(x+1)e-x,x∈(-∞,1)
④f(x)=xlnx,x∈(0,$\frac{1}{e}$)
以上函数为区间D上的“H函数”的序号是①②(写出所有正确的序号)
分析 不等式x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1)等价为(x1-x2)[f(x1)-f(x2)]>0,即满足条件的函数为单调递增函数,判断函数的单调性即可得到结论.
解答 解:∵对于任意给定的不等实数x1,x2,不等式x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1)恒成立,
∴不等式等价为(x1-x2)[f(x1)-f(x2)]>0恒成立,
即函数f(x)是定义在R上的增函数,
①y=$\frac{1}{3}$x3-$\frac{1}{2}$x2+$\frac{1}{2}$x,(x∈R),
y′=x2-x+$\frac{1}{2}$>0,函数递增,
②y=3x+cosx-sinx,x∈(0,$\frac{π}{2}$),
y′=3-sinx-cosx=3-$\sqrt{2}$sin(x+$\frac{π}{4}$)>0,函数递增,
③f(x)=(x+1)e-x,x∈(-∞,1),
f′(x)=$\frac{x+2}{{e}^{x}}$,
显然函数在(-∞,-2)递增,在(-2,1)递减,
④f(x)=xlnx,x∈(0,$\frac{1}{e}$)
f′(x)=lnx+1<0,函数递减,
故答案为:①②.
点评 本题主要考查函数单调性的应用,将条件转化为函数的单调性的形式是解决本题的关键.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
11.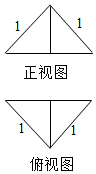 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )
 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图和俯视图如图所示,则其几何体的表面积为( )| A. | $\frac{2+\sqrt{2}}{2}$ | B. | $\frac{2+\sqrt{3}}{2}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
16.已知复数z满足z=i(1-i),(i为虚数单位)则|z|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
13.若X~B(n,$\frac{1}{3}$),且D(X)=$\frac{2}{3}$,则P(0≤X≤2)等于( )
| A. | $\frac{1}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{26}{27}$ | D. | $\frac{1}{27}$ |
6.若cos(α$+\frac{4π}{15}$)=$\frac{4}{5}$,则sin(2α$+\frac{31π}{30}$)=( )
| A. | $\frac{3}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{5}$ |
7.已知a=0.92,b=20.9,c=log20.9,则a,b,c的大小关系为( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |