题目内容
16．
如图，网络纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的表面积为（| A． | 17π | B． | 22π | C． | 68π | D． | 88π |
分析 由已知三视图得到几何体是长宽高分别为2，2，3的长方体，计算其体对角线长度，得知其外接球的直径，计算球表面积．
解答 解：原因是得到几何体是长宽高分别为2，2，3的长方体，所以外接球的直径为$\sqrt{{2}^{2}+{2}^{2}+{3}^{2}}=\sqrt{17}$，所以外接球表面积为：4π（$\sqrt{17}$）2=68π；
故选C．
点评 本题考查了由几何体的三视图求外接球的表面积；关键是还原几何体，明确外接球的半径．
练习册系列答案
相关题目
1．已知集合M={ x|x≥-$\frac{1}{2}$}，N={x|1-x2≥0}，则M∪N=（ ）
| A． | [-$\frac{1}{2}$，1] | B． | [-1，1] | C． | （-1，+∞） | D． | [-1，+∞） |
11．
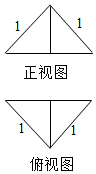把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥A-BCD的正视图和俯视图如图所示，则其几何体的表面积为（ ）
把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥A-BCD的正视图和俯视图如图所示，则其几何体的表面积为（ ）| A． | $\frac{2+\sqrt{2}}{2}$ | B． | $\frac{2+\sqrt{3}}{2}$ | C． | 1+$\sqrt{2}$ | D． | 1+$\sqrt{3}$ |
1．“∵四边形ABCD是矩形，∴四边形ABCD的对角线相等，”以上推理的大前提是（ ）
| A． | 四边形的对角线相等 | B． | 矩形的对角线相等 | ||
| C． | 矩形是四边形 | D． | 对角线相等的四边形是矩形 |
5．若两平行直线3x+4y-2a=0与3x+4y+1=0之间的距离为1，则a等于（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |