题目内容

16．已知直线l1：mx+y+1=0，l2：（m-3）x+2y-1=0，则“m=1”是“l1⊥l2”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 由l1⊥l2，可得-m×$（-\frac{m-3}{2}）$=-1，解得m即可判断出结论．

解答 解：∵“l1⊥l2”，∴-m×$（-\frac{m-3}{2}）$=-1，化为：m2-3m+2=0，
解得m=1，2．
∴“m=1”是“l1⊥l2”的充分不必要条件．
故选：A．

点评 本题考查了直线垂直与斜率的关系、方程的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
6．已知a，b，c为正实数，且a+b+c=3，证明：$\frac{{c}^{2}}{a}$+$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{c}$≥3．
7．已知向量$\overrightarrow{a}$=（sin（π+ωx），2cosωx），$\overrightarrow{b}$=（2$\sqrt{3}$sin（$\frac{π}{2}$+ωx），cosωx），（ω＞0），函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$，其图象上相邻的两个最低点之间的距离为π．
（Ⅰ）求函数f（x）的对称中心；
（Ⅱ）在锐角△ABC中，角A、B、C的对边分别为a、b、c，tanB=$\frac{\sqrt{3}ac}{{a}^{2}+{c}^{2}-{b}^{2}}$，求f（A）的取值范围．
4．若函数f（x）=$\frac{1}{2}{x^2}$-mx+lnx有极值，则函数f（x）的极值之和的取值范围是（-∞，-3）．
11．设集合A={y|y=2x，-1＜x＜2}，B={x|（x-1）（x+2）＜0}，则A∩B=（　　）
A．（-2，3）B．（-2，1）C．$（\frac{1}{2}，2）$D．$（\frac{1}{2}，1）$
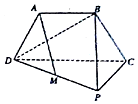1．如图，三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直，AB=AD=$\frac{1}{2}$CD，AB∥CD，CP⊥CD，M为PD的中点．
（1）求证：AM∥平面PBC；
（2）求证：平面BDP⊥平面PBC．
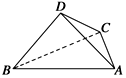8．如图所示，四面体ABCD中，已知平面BCD⊥平面ABC，BD⊥DC，BC=6，AB=4$\sqrt{3}$，∠ABC=30°．
（I）求证：AC⊥BD；
（II）若二面角B-AC-D为45°，求直线AB与平面ACD所成的角的正弦值．
5．已知向量$\overrightarrow{a}$=（3，-1），$\overrightarrow{b}$=（2，1），则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为$\sqrt{5}$．
20．已知在一次全国数学竞赛中，某市3000名参赛学生的初赛成绩统计如图所示．则在本次数学竞赛中，成绩在[80，90]上的学生人数为900．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网