题目内容
1.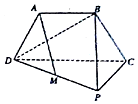 如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=$\frac{1}{2}$CD,AB∥CD,CP⊥CD,M为PD的中点.
如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=$\frac{1}{2}$CD,AB∥CD,CP⊥CD,M为PD的中点.(1)求证:AM∥平面PBC;
(2)求证:平面BDP⊥平面PBC.
分析 (1)取PC的中点N,连结MN,BN,则四边形ABNM是平行四边形,得出AM∥BN,故而AM∥平面PBC;
(2)由面面垂直得PC⊥BD,由等腰梯形的性质可得BD⊥BC,故而BD⊥平面PBC,于是平面BDP⊥平面PBC.
解答  证明:(1)取PC的中点N,连结MN,BN,
证明:(1)取PC的中点N,连结MN,BN,
则MN$\stackrel{∥}{=}$$\frac{1}{2}$CD,又AB$\stackrel{∥}{=}$$\frac{1}{2}$CD,
∴四边形ABNM是平行四边形,
∴AM∥BN,又AM?平面PBC,BN?平面PBC,
∴AM∥平面PBC.
(2)∵平面ABCD⊥平面PCD,平面ABCD∩平面PCD=CD,CD⊥PC,PC?平面PCD,
∴PC⊥平面ABCD,∵BD?平面ABCD,
∴BD⊥PC,
∵四边形ABCD是等腰梯形,AD=AB=BC=$\frac{1}{2}$CD,
则cos∠BCD=$\frac{\frac{1}{2}(CD-AB)}{BC}$=$\frac{1}{2}$,即∠BCD=60°,
∴BD2=BC2+CD2-BC•CD=3BC2,∴BC2+BD2=CD2,
∴BD⊥BC,
又BC∩PC=C,BC?平面PBC,PC?平面PBC,
∴BD⊥平面PBC,又BD?平面PBD,
∴平面PBD⊥平面PBC.
点评 本题考查了线面平行的判定,面面垂直的性质与判定,属于中档题.

练习册系列答案
相关题目
16.已知直线l1:mx+y+1=0,l2:(m-3)x+2y-1=0,则“m=1”是“l1⊥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.设x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$,目标函数z=ax+by(a>0,b>0)的最大值为M,若M的取值范围是[1,2],则点M(a,b)所经过的区域面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
13.如图是一个算法流程图,则输出的x值为( )


| A. | 95 | B. | 47 | C. | 23 | D. | 11 |
10.已知i为虚数单位,z(1-i)=1+i,则复数z的共轭复数为( )
| A. | -i | B. | i | C. | 2i | D. | -2i |
5.为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房的心理预期调研,用简单随机抽样的方法抽取110人进行统计,得到如下列联表:
已知样本中城市人数与农村人数之比是3:8.
(1)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(2)用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$.
| 买房 | 不买房 | 纠结 | |
| 城市人 | 5 | 15 | |
| 农村人 | 20 | 10 |
(1)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(2)用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$.
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
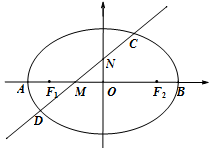 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.