题目内容
6.已知a,b,c为正实数,且a+b+c=3,证明:$\frac{{c}^{2}}{a}$+$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{c}$≥3.分析 由基本不等式,得$\frac{{c}^{2}}{a}$+a≥2c,$\frac{{a}^{2}}{b}$+b≥2a,$\frac{{b}^{2}}{c}$+c≥2b,相加即可证明.
解答 证:因为a,b,c为正实数,
所以由基本不等式,得$\frac{{c}^{2}}{a}$+a≥2c,$\frac{{a}^{2}}{b}$+b≥2a,$\frac{{b}^{2}}{c}$+c≥2b,当且仅当a=b=c=1时取等号
三式相加,得:$\frac{{c}^{2}}{a}$+$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{c}$≥a+b+c.
又a+b+c=3,
所以$\frac{{c}^{2}}{a}$+$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{c}$≥3.
点评 本题考查了不等式的证明,关键是掌握基本不等式成立的条件,一正二定三相等,属于中档题

练习册系列答案
相关题目
16.设α为锐角,且cos(α+$\frac{π}{6}$)=$\frac{3}{5}$.
(1)求cos($α-\frac{π}{3}$)的值;
(2)求cos(2α-$\frac{π}{6}$)的值.
(1)求cos($α-\frac{π}{3}$)的值;
(2)求cos(2α-$\frac{π}{6}$)的值.
17.若|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,|$\overrightarrow{c}$|=$\sqrt{3}$,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,则$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$的最大值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
18.定义在区间(0,$\frac{π}{2}$)上的函数y=6cosx的图象与y=5tanx的图象的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图象交于点P2,则线段P1P2的长为( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
15.命题p:将函数y=cosx•sinx的图象向右平移$\frac{3π}{4}$个单位可得到y=$\frac{1}{2}$cos2x的图象;命题q:对?m>0,双曲线2x2-y2=m2的离心率为$\sqrt{3}$,则下列结论正确的是( )
| A. | p是假命题 | B. | ¬p是真命题 | C. | p∨q是真命题 | D. | p∧q是假命题 |
16.已知直线l1:mx+y+1=0,l2:(m-3)x+2y-1=0,则“m=1”是“l1⊥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
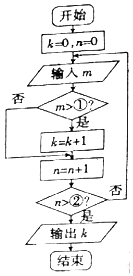 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是14,19.
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是14,19.