题目内容
8.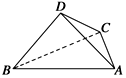 如图所示,四面体ABCD中,已知平面BCD⊥平面ABC,BD⊥DC,BC=6,AB=4$\sqrt{3}$,∠ABC=30°.
如图所示,四面体ABCD中,已知平面BCD⊥平面ABC,BD⊥DC,BC=6,AB=4$\sqrt{3}$,∠ABC=30°.(I)求证:AC⊥BD;
(II)若二面角B-AC-D为45°,求直线AB与平面ACD所成的角的正弦值.
分析 (I)利用余弦定理计算AC,得出AC⊥BC,再利用面面垂直的性质得出AC⊥平面BCD,从而有AC⊥BD;
(II)证明BD⊥平面ACD,于是∠BAD为所求角,先计算BD,在Rt△ABD中计算sin∠BAD.
解答 (I)证明:△ABC中,由余弦定理得AC2=36+48-2×$6×4\sqrt{3}×cos30°$=12,
∴$AC=2\sqrt{3}$,∴AC2+BC2=AB2,∴AC⊥BC.
又平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,AC?平面ABC,
∵AC⊥平面BCD.又∵BD?平面BCD,
∴AC⊥BD.
(II)解:∵AC⊥平面BCD,CD?平面BCD,
∴AC⊥CD.又∵BC⊥AC,
∴∠BCD是平面DAC与平面BAC所成的二面角的平面角,即∠BCD=45°.
∵BD⊥CD,AC⊥BD,CD?平面ACD,AC?平面ACD,CD∩AC=C,
∴BD⊥平面ACD.
∴∠BAD是AB与平面ACD所成的角.
Rt△ACD中,$BD=BCsin{45°}=3\sqrt{2}$,
∴$sin∠BAD=\frac{BD}{AB}=\frac{{\sqrt{6}}}{4}$.
即求直线AB与平面ACE所成的角的正弦值为$\frac{{\sqrt{6}}}{4}$.
点评 本题考查了线面垂直的判定,空间角的计算,属于中档题.

练习册系列答案
相关题目
18.定义在区间(0,$\frac{π}{2}$)上的函数y=6cosx的图象与y=5tanx的图象的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图象交于点P2,则线段P1P2的长为( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
16.已知直线l1:mx+y+1=0,l2:(m-3)x+2y-1=0,则“m=1”是“l1⊥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.如图是一个算法流程图,则输出的x值为( )


| A. | 95 | B. | 47 | C. | 23 | D. | 11 |
17.若(3x-1)5=a0+a1x+a2x2+…+a5x5,则a1+2a2x+3a3x+4a4+5a5=( )
| A. | 80 | B. | 120 | C. | 180 | D. | 240 |
12.下列函数中,与函数y=-3|x|的奇偶性相同,且在(-∞,0)上单调性也相同的是( )
| A. | y=1-x2 | B. | y=log2|x| | C. | y=-$\frac{1}{x}$ | D. | y=x3-1 |