题目内容
4.若函数f(x)=$\frac{1}{2}{x^2}$-mx+lnx有极值,则函数f(x)的极值之和的取值范围是(-∞,-3).分析 先求导,方程x2-mx+1=0在(0,+∞)上有根求出m的范围,根据韦达定理即可化简f(x1)+f(x2),根据m的范围即可求出.
解答 解:∵f(x)的定义域是(0,+∞),
f′(x)=x-m+$\frac{1}{x}$=$\frac{{x}^{2}-mx+1}{x}$,
∵f(x)存在极值,
∴f′(x)=0在(0,+∞)上有根,
即方程x2-mx+1=0在(0,+∞)上有根.
设方程x2-mx+1=0的两根为x1,x2,
∴△=m2-4>0,x1+x2=m>0,x1x2=1
即m>2
∴f(x1)+f(x2)=$\frac{1}{2}$(x12+x22)-m(x1+x2)+(lnx1+lnx2),
=$\frac{1}{2}$(x1+x2)2-x1x2-m(x1+x2)+lnx1x2,
=$\frac{1}{2}$m2-1-m2,
=-$\frac{1}{2}$m2-1<-3,
故函数f(x)的极值之和的取值范围是(-∞,-3)
故答案为:(-∞,-3)
点评 本题考查了导数函数极值的关系,以及韦达定理及二次函数的性质,考查了分析问题解决问题的能力,属于中档题

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
15.命题p:将函数y=cosx•sinx的图象向右平移$\frac{3π}{4}$个单位可得到y=$\frac{1}{2}$cos2x的图象;命题q:对?m>0,双曲线2x2-y2=m2的离心率为$\sqrt{3}$,则下列结论正确的是( )
| A. | p是假命题 | B. | ¬p是真命题 | C. | p∨q是真命题 | D. | p∧q是假命题 |
16.已知直线l1:mx+y+1=0,l2:(m-3)x+2y-1=0,则“m=1”是“l1⊥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.如图是一个算法流程图,则输出的x值为( )


| A. | 95 | B. | 47 | C. | 23 | D. | 11 |
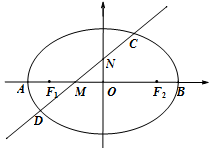 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.