题目内容
若“对任意的实数x，不等式x2+2x+a＞0均成立”是假命题，则实数a的取值范围（ ）
| A、（1，+∞） |
| B、[1，+∞） |
| C、（-∞，1） |
| D、（-∞，1] |
考点：全称命题
专题：函数的性质及应用,简易逻辑
分析：由“对任意的实数x，不等式x2+2x+a＞0均成立”是假命题，可得x2+2x+a=0的△≥0，进而可得实数a的取值范围．
解答：
解：∵“对任意的实数x，不等式x2+2x+a＞0均成立”是假命题，
故“存在实数x，使x2+2x+a≤0成立”，
∴x2+2x+a=0的△=4-4a≥0，
解得：a∈（-∞，1]，
故选：D
故“存在实数x，使x2+2x+a≤0成立”，
∴x2+2x+a=0的△=4-4a≥0，
解得：a∈（-∞，1]，
故选：D
点评：本题考查的知识点是全称命题与特称命题，二次函数的图象与性质，难度不大，属于基础题．
练习册系列答案
相关题目
方程lnx+2x=6的根属于区间（ ）
| A、（1，2） | ||||
B、（
| ||||
C、（1，
| ||||
D、（
|
函数y=
的图象大致为（ ）
| cos3x |
| 3x-3-x |
A、 |
B、 |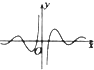
C、 |
D、 |
已知集合A={x|log2（x+2）＞1}，B={x|（
）x＞
}，则A∩∁RB=（ ）
| 1 |
| 2 |
| 1 |
| 4 |
| A、（2，+∞） |
| B、[2，+∞） |
| C、（0，2） |
| D、（0，2] |