题目内容
如果方程x2-ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是 .
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据题意,x2+ky2=2化为标准形式;由椭圆的标准方程,要使其表示焦点在y轴上的椭圆,推出不等式;计算可得答案.
解答:
解:根据题意,x2-ky2=2化为标准形式为
+
=1;
根据题意,其表示焦点在y轴上的椭圆,则有-
>2;
解可得-1<k<0;
故答案为:-1<k<0.
| y2 | ||
|
| x2 |
| 2 |
根据题意,其表示焦点在y轴上的椭圆,则有-
| 2 |
| k |
解可得-1<k<0;
故答案为:-1<k<0.
点评:本题考查椭圆的标准方程,注意椭圆与双曲线的标准方程都可以由二元二次方程表示,但要区分两者形式的不同;其次注意焦点位置不同时,参数a、b大小的不同.

练习册系列答案
相关题目
某算法的程序如图所示,若输入x=2,则电脑屏上显示的结果为( )


| A、16 | B、4 | C、y=0 | D、0 |
若“对任意的实数x,不等式x2+2x+a>0均成立”是假命题,则实数a的取值范围( )
| A、(1,+∞) |
| B、[1,+∞) |
| C、(-∞,1) |
| D、(-∞,1] |
已知某几何体的三视图如图所示,则该几何体的体积等于( )


A、
| ||
| B、32 | ||
C、
| ||
D、
|
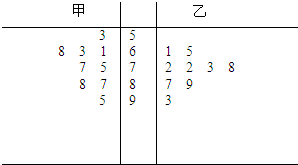 某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图
某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图