题目内容
20. 如图,在三棱锥K-ABC中,平面KAC⊥平面ABC,KC⊥AC,AC⊥AB,H为KA的中点,KC=AC=AB=2.
如图,在三棱锥K-ABC中,平面KAC⊥平面ABC,KC⊥AC,AC⊥AB,H为KA的中点,KC=AC=AB=2.(Ⅰ)求证:CH⊥平面KAB;
(Ⅱ)求二面角H-BC-A的余弦值;
(Ⅲ)若M为AC中点,在直线KB上是否存在点N使MN∥平面HBC,若存在,求出KN的长,若不存在,说明理由.
分析 (Ⅰ)由已知AB⊥平面KAC,从而AB⊥CH,由等腰三角形性质得CH⊥AK,由此能证明CH⊥平面AKB.
(Ⅱ)以A为原点,AB为x轴,AC为y轴,过A垂直于平面ABCD的直线AD为z轴,建立空间直角坐标系,由此利用向量法能求出二面角H-BC-A的余弦值.
(Ⅲ)$设\overrightarrow{KN}=λ\overrightarrow{KB}$,N(a,b,c),利用向量法能求出在直线KB上存在点N使MN∥平面HBC,并能求出KN的长.
解答  证明:(Ⅰ)因为平面KAC⊥底面ABC,且AB垂直于这两个平面的交线AC,
证明:(Ⅰ)因为平面KAC⊥底面ABC,且AB垂直于这两个平面的交线AC,
所以AB⊥平面KAC…(1分)
所以AB⊥CH…(2分)
因为CK=CA,H为AK中点,所以CH⊥AK…(3分)
因为AB∩AK=A,所以CH⊥平面AKB.…(4分)
解:(Ⅱ)如图,以A为原点,AB为x轴,AC为y轴,过A垂直于平面ABCD的直线AD为z轴,建立空间直角坐标系,
则A(0,0,0),K(0,2,2),H(0,1,1),C(0,2,0),B(2,0,0)
$所以\overrightarrow{CH}=(0,-1,1),\overrightarrow{BC}=(-2,2,0)$,
$设平面HBC的法向量为\overrightarrow n=(x,y,z)$,…(1分)
$则\left\{{\begin{array}{l}{\overrightarrow{CH}•\overrightarrow n=0}\\{\overrightarrow{BC}•\overrightarrow n=0}\end{array}}\right.$,即$\left\{{\begin{array}{l}{-y+z=0}\\{-2x+2y=0}\end{array}}\right.$,
$令y=1,则z=1,x=1.所以\overrightarrow n=(1,1,1)$…(3分)
$取平面ABC的法向量为\overrightarrow m=(0,0,1)$…(4分)
$cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overrightarrow n}{|\overrightarrow m|•|\overrightarrow n|}=\frac{1}{{\sqrt{3}}}=\frac{{\sqrt{3}}}{3}$…(5分)
因为所求的二面角为锐角,
$所以二面角H-BC-A的余弦值为\frac{{\sqrt{3}}}{3}$.…(6分)
(Ⅲ)$设\overrightarrow{KN}=λ\overrightarrow{KB}$,N(a,b,c),…(1分)
$\begin{array}{l}则(a,b-2,c-2)=(2λ,-2λ,-2λ)\\ 所以\left\{{\begin{array}{l}{a=2λ}\\{b=2-2λ}\\{c=2-2λ}\end{array}}\right.\end{array}$
所以N(2λ,2-2λ,2-2λ)因为M(0,1,0),
$所以\overrightarrow{MN}=(2λ,1-2λ,2-2λ)$…(2分)
$由\overrightarrow{MN}•\overrightarrow n=0$,得3-2λ=0,$所以λ=\frac{3}{2}$.…(3分)
$|\overrightarrow{KN}|=|\frac{3}{2}\overrightarrow{KB}|=\frac{3}{2}|\overrightarrow{KB}|=\frac{3}{2}×2\sqrt{3}=3\sqrt{3}$.
$所以直线KB上存在点N,KN的长为3\sqrt{3}$.…(4分)
点评 本题考查线面垂直的证明,考查面角的余弦值的求法,考查满足条件的点是否存在的判断与求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 名校课堂系列答案
名校课堂系列答案| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
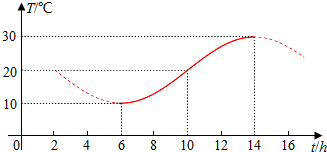
| A. | 25°C | B. | 26°C | C. | 27°C | D. | 28°C |