题目内容
5.用秦九韶算法计算函数f(x)=2x5+3x4+2x3-4x+5当x=2时的函数值.分析 根据秦九韶算法,把多项式改写成如下形式:f(x)=((((2x+3)x+2)x+0)x-4)x+5.从内到外的顺序依次计算一次多项式当x=2时的值:v0;v1;v2;v3;
v4;v5.即可得出.
解答 解:根据秦九韶算法,把多项式改写成如下形式:
f(x)=((((2x+3)x+2)x+0)x-4)x+5.
从内到外的顺序依次计算一次多项式当x=2时的值:
v0=2;
v1=2×2+3=7;
v2=v1×2+2=16;
v3=v2×2+0=32;
v4=v3×2-4=60;
v5=v4×2+5=125.
所以,当x=2时,多项式的值等于125.
点评 本题考查了秦九韶算法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.将八进制数26(8)转化为十进制数,结果是( )
| A. | 20 | B. | 22 | C. | 24 | D. | 26 |
20.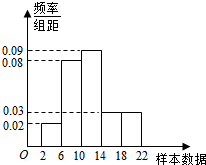 样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是( )
样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是( )
 样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是( )
样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是( )| A. | 32,0.4 | B. | 8,0.1 | C. | 32,0.1 | D. | 8,0.4 |
10.m<n<0是$\frac{1}{m}$>$\frac{1}{n}$成立的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中A>0,ω>0,-π<φ<π),那么中午12时温度的近似值(精确到1°C)是( )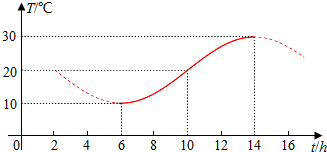

| A. | 25°C | B. | 26°C | C. | 27°C | D. | 28°C |