题目内容
已知圆O:x2+y2=50与直线l:x-2y-5=0相交于A,B两点(点A的横坐标大于点B的横坐标),求:
(1)A,B的坐标;
(2)△ABO的面积.
(1)A,B的坐标;
(2)△ABO的面积.
考点:直线与圆的位置关系
专题:直线与圆
分析:(1)联立直线方程和圆的方程解方程组即可求出A,B的坐标;
(2)求出|AB|的长度,利用点到直线的距离求出三角形的高,即可求△ABO的面积.
(2)求出|AB|的长度,利用点到直线的距离求出三角形的高,即可求△ABO的面积.
解答:
解:(1)由
,解得
或
,
即交点坐标为(7,1),和(-5,-5),
∵点A的横坐标大于点B的横坐标,
∴A(7,1),B(-5,-5);
(2)∵A(7,1),B(-5,-5);
∴|AB|=
=
=3
,
圆心O到直线x-2y-5=0的距离d=
=
=
,
则△ABO的面积S=
×3
×
=15.
|
|
|
即交点坐标为(7,1),和(-5,-5),
∵点A的横坐标大于点B的横坐标,
∴A(7,1),B(-5,-5);
(2)∵A(7,1),B(-5,-5);
∴|AB|=
| (-5-7)2+(-5-1)2 |
| 122+62 |
| 20 |
圆心O到直线x-2y-5=0的距离d=
| |-5| | ||
|
| 5 | ||
|
| 5 |
则△ABO的面积S=
| 1 |
| 2 |
| 20 |
| 5 |
点评:本题主要考查直线和圆的位置关系,利用点到直线的距离求出三角形的高是解决本题的关键.

练习册系列答案
相关题目
已知l1:x+2y+1=0,l2:Ax+By+2=0(A,B∈{1,2,3,4}),则直线l1与l2不平行的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若一个球的体积为
π,则该球的表面积为( )
| 9 |
| 2 |
A、
| ||
B、
| ||
| C、18π | ||
| D、9π |
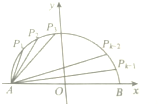 如图,AB是圆x2+y2=16的直径,把线段AB分成k(k≥4,k∈Z)等份,过每个分点作x轴的垂线交圆的上半部分于P1,P2,…,Pk-1,共k-1个点,令an=|APn|,n=1,2,3,…,k-1.则( )
如图,AB是圆x2+y2=16的直径,把线段AB分成k(k≥4,k∈Z)等份,过每个分点作x轴的垂线交圆的上半部分于P1,P2,…,Pk-1,共k-1个点,令an=|APn|,n=1,2,3,…,k-1.则( )| A、{an}是等差数列 |
| B、{an}是等比数列 |
| C、当k=8时,a12+a22+a32+…+a72=224 |
| D、当k=8时,a1+a2+a3+…+a7=224 |
圆x2+y2-4x+2y+F=0与y轴交于A,B两点,圆心为C.若∠ACB=90°,则F的值等于( )
A、-2
| ||
B、2
| ||
| C、3 | ||
| D、-3 |