Question

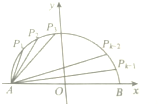如图，AB是圆x²+y²=16的直径，把线段AB分成k（k≥4，k∈Z）等份，过每个分点作x轴的垂线交圆的上半部分于P₁，P₂，…，P_k-1，共k-1个点，令a_n=|AP_n|，n=1，2，3，…，k-1．则（　　）

• A、{a_n}是等差数列
• B、{a_n}是等比数列
• C、当k=8时，a₁²+a₂²+a₃²+…+a₇²=224
• D、当k=8时，a₁+a₂+a₃+…+a₇=224

Answer 1

考点：等差关系的确定,等比关系的确定

专题：等差数列与等比数列

分析：依题意知，a₁=|AP₁|=|BP_k-1|，作出图形，由于AB是圆x²+y²=16的直径，易得a12+ak-12=64，从而可得答案．

解答： 解：依题意知，a₁=|AP₁|=|BP_k-1|，
又|AP_k-1|²+|BP_k-1|²=|AB|²=8²=64，即a12+ak-12=64，
∴当k=8时，令S₇=a₁²+a₂²+a₃²+…+a₇²，
则S₇=a₇²+a₆²+a₅²+…+a₁²，
两式相加得：2S₇=（a₁²+a₇²）+（a₂²+a₆²）+…+（a₇²+a₁²）=7×64=448，
∴S₇=224
故选：C．

点评：本题考查数列的求和，分析得到a12+ak-12=64是关键，考查作图与观察、分析、解决问题的能力，属于中档题．