题目内容
圆x2+y2-4x+2y+F=0与y轴交于A,B两点,圆心为C.若∠ACB=90°,则F的值等于( )
A、-2
| ||
B、2
| ||
| C、3 | ||
| D、-3 |
考点:直线与圆相交的性质
专题:直线与圆
分析:求出圆心和半径,根据∠ACB=90°点到圆心到直线的距离即可得到结论.
解答:
解:圆的标准方程为(x-2)2+(y+1)2=5-F,
则圆心为C(2,-1),半径R=
,(F<5),
若若∠ACB=90°,则圆心到y的距离d=Rsin45°=
×
,
即2=
×
,
解得F=-3,
故选:D.
则圆心为C(2,-1),半径R=
| 5-F |
若若∠ACB=90°,则圆心到y的距离d=Rsin45°=
| ||
| 2 |
| 5-F |
即2=
| ||
| 2 |
| 5-F |
解得F=-3,
故选:D.
点评:本题主要考查直线和圆的位置关系的应用,求出圆心和半径是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,△O′A′B′为斜二测画法做出的△OAB的直观图,其中O′A′=A′B′=2则原△OAB的面积是( )
如图所示,△O′A′B′为斜二测画法做出的△OAB的直观图,其中O′A′=A′B′=2则原△OAB的面积是( )A、2
| ||
| B、4 | ||
C、4
| ||
| D、8 |
已知函数f(x)=
,则不等式f(x)-x≥0的解集为( )
|
| A、(-∞,-3]∪[0,1) |
| B、[-3,0] |
| C、(-∞,-3]∪[0,+∞) |
| D、[-3,+∞) |
抛物线y=
x2,下列描述正确的是( )
| 1 |
| 4 |
| A、开口向右,焦点为(1,0) | ||
B、开口向上,焦点为(0,
| ||
| C、开口向右,准线为x=-1 | ||
| D、开口向上,准线为y=-1 |
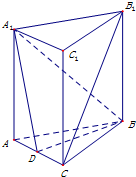 如图,在直三棱柱ABC-A1B1C1中,cos∠A1DD1=
如图,在直三棱柱ABC-A1B1C1中,cos∠A1DD1=