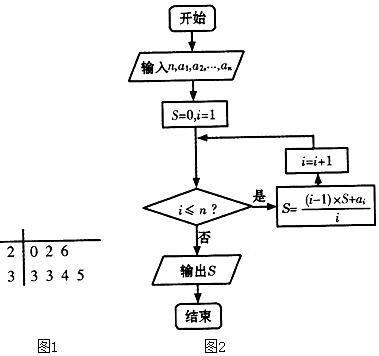
题目内容
18.某学校有高一、高二、高三三个年级,已知高一、高二、高三的学生数之比为2:3;5,现从该学校中抽取一个容量为100的样本,从高一学生中用简单随机抽样抽取样本时,学生甲被抽到的概率为$\frac{1}{4}$,则该学校学生的总数为( )| A. | 200 | B. | 400 | C. | 500 | D. | 1000 |
分析 求出在整个抽样过程中,每个学生被抽到的概率为$\frac{1}{4}$,从该学校中抽取一个容量为100的样本,可得该学校学生的总数.
解答 解:∵从高一学生中用简单随机抽样抽取样本时,学生甲被抽到的概率为$\frac{1}{4}$,
∴在整个抽样过程中,每个学生被抽到的概率为$\frac{1}{4}$,
∵从该学校中抽取一个容量为100的样本,
∴该学校学生的总数为$\frac{100}{\frac{1}{4}}$=400,
故选:B.
点评 本题考查分层抽样,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
8.已知各项均不相等的等比数列{an}中,a2=1,且$\frac{1}{4}$a1,a3,$\frac{7}{4}$a5成等差数列,则a4等于( )
| A. | $\frac{1}{49}$ | B. | 49 | C. | $\frac{1}{7}$ | D. | 7 |
6.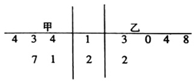 2017年3月2日至16日,全国两会在北京召开,甲、乙两市近5年与会代表名额数统计如图所示,设甲、乙的数据平均数分别为$\overline{{x}_{1}}$,$\overline{{x}_{2}}$,中位数分别为y1,y2,则( )
2017年3月2日至16日,全国两会在北京召开,甲、乙两市近5年与会代表名额数统计如图所示,设甲、乙的数据平均数分别为$\overline{{x}_{1}}$,$\overline{{x}_{2}}$,中位数分别为y1,y2,则( )
 2017年3月2日至16日,全国两会在北京召开,甲、乙两市近5年与会代表名额数统计如图所示,设甲、乙的数据平均数分别为$\overline{{x}_{1}}$,$\overline{{x}_{2}}$,中位数分别为y1,y2,则( )
2017年3月2日至16日,全国两会在北京召开,甲、乙两市近5年与会代表名额数统计如图所示,设甲、乙的数据平均数分别为$\overline{{x}_{1}}$,$\overline{{x}_{2}}$,中位数分别为y1,y2,则( )| A. | $\overline{{x}_{1}}$>$\overline{{x}_{2}}$,y1>y2 | B. | $\overline{{x}_{1}}$>$\overline{{x}_{2}}$,y1=y2 | C. | $\overline{{x}_{1}}$<$\overline{{x}_{2}}$,y1=y2 | D. | $\overline{{x}_{1}}$<$\overline{{x}_{2}}$,y1<y2 |
7.已知全集U={x∈N|x≤4},A={0,1,3},B={1,3,4},则∁U(A∩B)=( )
| A. | {2} | B. | {4} | C. | {2,4} | D. | {0,2,4} |
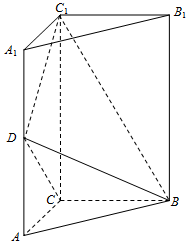 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠ACB=90°,AC=BC=1,AA1=2,D是棱AA1的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠ACB=90°,AC=BC=1,AA1=2,D是棱AA1的中点.