题目内容
13.某品牌洗衣机专柜在国庆期间举行促销活动,茎叶图1中记录了每天的销售量(单位:台),把这些数据经过如图2所示的程序框图处理后,输出的S=( )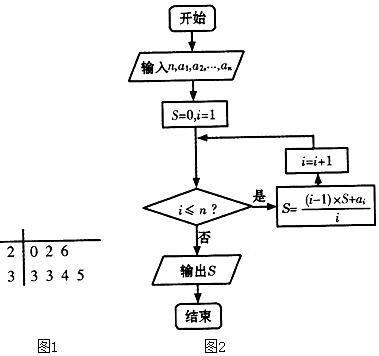
| A. | 196 | B. | 203 | C. | 28 | D. | 29 |
分析 由茎叶图可知n=7,模拟程序的运行,依次写出每次循环得到的S,i的值,当i=8时不满足条件i≤7,退出循环,输出S的值为29.
解答 解:由茎叶图可知n=7,
模拟程序的运行,可得
S=0,i=1
满足条件i≤7,执行循环体,S=20,i=2
满足条件i≤7,执行循环体,S=$\frac{20+22}{2}$=21,i=3
满足条件i≤7,执行循环体,S=$\frac{2×21+26}{3}$=$\frac{68}{3}$,i=4
满足条件i≤7,执行循环体,S=$\frac{3×\frac{68}{3}+33}{4}$=$\frac{101}{4}$,i=5
满足条件i≤7,执行循环体,S=$\frac{4×\frac{101}{4}+33}{5}$=$\frac{134}{5}$,i=6
满足条件i≤7,执行循环体,S=$\frac{5×\frac{134}{5}+34}{6}$=$\frac{168}{6}$,i=7
满足条件i≤7,执行循环体,S=$\frac{6×\frac{168}{6}+35}{7}$=29,i=8
不满足条件i≤7,退出循环,输出S的值为29.
故选:D.
点评 本题主要考查了茎叶图及循环结构的程序框图的应用,模拟程序的运行正确得到每次循环时S,i的值是解题的关键,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.f(x)=$\sqrt{x}$lnx在点(4,f(4))处的切线方程为( )
| A. | (ln2+1)x-2y+4ln2-4=0 | B. | (ln4+1)x-2y+7ln4-1=0 | ||
| C. | (ln4+1)x-2y+8ln2-4=0 | D. | (ln2+1)x+2y+7ln2-4=0 |
18.某学校有高一、高二、高三三个年级,已知高一、高二、高三的学生数之比为2:3;5,现从该学校中抽取一个容量为100的样本,从高一学生中用简单随机抽样抽取样本时,学生甲被抽到的概率为$\frac{1}{4}$,则该学校学生的总数为( )
| A. | 200 | B. | 400 | C. | 500 | D. | 1000 |
11.在正项等比数列{an}和正项等差数列{bn}中,已知a1,a2017的等比中项与b1,b2017的等差中项相等,且$\frac{1}{{b}_{1}}$+$\frac{4}{{b}_{2017}}$≤1,当a1009取得最小值时,等差数列{bn}的公差d的取值集合为( )
| A. | {d|d≥$\frac{1}{672}$} | B. | {d|0<d<$\frac{1}{672}$} | C. | {$\frac{1}{672}$} | D. | {d|d≥$\frac{3}{2017}$} |