题目内容

6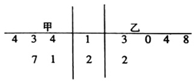．2017年3月2日至16日，全国两会在北京召开，甲、乙两市近5年与会代表名额数统计如图所示，设甲、乙的数据平均数分别为$\overline{{x}_{1}}$，$\overline{{x}_{2}}$，中位数分别为y1，y2，则（　　）
A．$\overline{{x}_{1}}$＞$\overline{{x}_{2}}$，y1＞y2B．$\overline{{x}_{1}}$＞$\overline{{x}_{2}}$，y1=y2C．$\overline{{x}_{1}}$＜$\overline{{x}_{2}}$，y1=y2D．$\overline{{x}_{1}}$＜$\overline{{x}_{2}}$，y1＜y2

分析 根据茎叶图分别判断甲、乙的最高分和最低分，利用平均数公式及中位数的定义分别求出甲、乙的平均数与中位数，可得答案．

解答 解：由茎叶图知甲的最高分为27，最低分为13，则$\overline{{x}_{1}}$=$\frac{14+13+14+21+27}{5}$=17.8，中位数y1=14；
由茎叶图知乙的最高分为22，最低分为10，则$\overline{{x}_{2}}$=$\frac{13+10+14+18+22}{5}$=15.4，中位数y2=14，
所以$\overline{{x}_{1}}$＞$\overline{{x}_{2}}$，y1=y2．
故选：B．

点评 本题考查了利用茎叶图求数据的平均数与中位数．

练习册系列答案
相关题目
16．已知数列{an}，{bn}的首项a1=b1=1，且满足（an+1-an）2=4，|bn+1|=q|bn|，其中n∈N*．设数列{an}，{bn}的前n项和分别为Sn，Tn．
（Ⅰ）若不等式an+1＞an对一切n∈N*恒成立，求Sn；
（Ⅱ）若常数q＞1且对任意的n∈N*，恒有$\sum_{k=1}^{n+1}$|bk|≤4|bn|，求q的值；
（Ⅲ）在（2）的条件下且同时满足以下两个条件：
（ⅰ）若存在唯一正整数p的值满足ap＜ap-1；
（ⅱ） Tm＞0恒成立．试问：是否存在正整数m，使得Sm+1=4bm，若存在，求m的值；若不存在，请说明理由．
17．已知x，y满足$\left\{{\begin{array}{l}{y≥x，\;}\\{x+y≤4}\\{2x-y≥k}\end{array}}\right.$若z=x+2y有最大值8，则实数k的值为-4．
14．已知集合M={1，2，3，4，9}，N={x|x∈M且$\sqrt{x}$∈M}，则M∩N中的元素个数为（　　）
A．0B．1C．2D．3
1．设数列{an}的通项公式an=2n-1，数列{bn}满足a1b1+a2b2+a3b3+…+anbn=$\frac{20}{9}$+（$\frac{2n}{3}$-$\frac{5}{9}$）×2${\;}^{2n+{2}^{\;}}$，则数列{bn}的通项公式bn=4n．
11．如图1，四边形ABCD是菱形，且∠A=60°，AB=2，E为AB的中点，将四边形EBCD沿DE折起至EDC1B1，如图2．

（Ⅰ） 求证：平面ADE⊥平面AEB1；
（Ⅱ） 若二面角A-DE-C1的大小为$\frac{π}{3}$，求三棱锥C1-AB1D的体积．
18．某学校有高一、高二、高三三个年级，已知高一、高二、高三的学生数之比为2：3；5，现从该学校中抽取一个容量为100的样本，从高一学生中用简单随机抽样抽取样本时，学生甲被抽到的概率为$\frac{1}{4}$，则该学校学生的总数为（　　）
A．200B．400C．500D．1000
15．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点与抛物线y2=4$\sqrt{5}$x的焦点重合，点P（2，1）在双曲线的渐近线上，则ab的值为（　　）
A．2B．$\sqrt{2}$C．8D．$\frac{10}{3}$
4．求函数f（x）=x2+x在区间[x0，x0+△x]上的平均变化率，并求当x0=1，△x=0.1时的平均变化率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网