题目内容
已知f(x)=log
(x2-mx-m).
(1)若m=0,求函数f(x)的定义域;
(2)若f(x)的值域为R,求m的取值范围;
(3)若f(x)在区间(-∞,1-
)上是增函数,求实数m的取值范围.
| 1 |
| 2 |
(1)若m=0,求函数f(x)的定义域;
(2)若f(x)的值域为R,求m的取值范围;
(3)若f(x)在区间(-∞,1-
| 3 |
考点:复合函数的单调性,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)把m代入函数解析式,由对数式的真数大于0得答案;
(2)由真数可以取到大于0的所有数,则其判别式大于等于0,由此求解m的范围;
(3)由符合函数的单调性可得,内函数在(-∞,1-
)上是减函数,且在(-∞,1-
)上大于0恒成立,转化为不等式组得答案.
(2)由真数可以取到大于0的所有数,则其判别式大于等于0,由此求解m的范围;
(3)由符合函数的单调性可得,内函数在(-∞,1-
| 3 |
| 3 |
解答:
解:(1)当m=0时,f(x)=log
x2,当x≠0时,x2>0,
∴函数f(x)的定义域为{x|x≠0};
(2)若f(x)的值域为R,则函数t=x2-mx-m能够取到大于0的所有实数,
则(-m)2+4m≥0,解得m≤-4或m≥0.
∴m的取值范围是(-∞,-4]∪[0,+∞);
(3)若f(x)在区间(-∞,1-
)上是增函数,
即内函数t=x2-mx-m在(-∞,1-
)上是减函数,
∴
,解得:2-2
≤m≤2.
∴实数m的取值范围是[2-2
,2].
| 1 |
| 2 |
∴函数f(x)的定义域为{x|x≠0};
(2)若f(x)的值域为R,则函数t=x2-mx-m能够取到大于0的所有实数,
则(-m)2+4m≥0,解得m≤-4或m≥0.
∴m的取值范围是(-∞,-4]∪[0,+∞);
(3)若f(x)在区间(-∞,1-
| 3 |
即内函数t=x2-mx-m在(-∞,1-
| 3 |
∴
|
| 3 |
∴实数m的取值范围是[2-2
| 3 |
点评:本题考查了函数的定义域及其求法,考查了复合函数的单调性,考查了数学转化思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列语句中是命题的是( )
| A、正弦函数是周期函数吗? | ||||
B、sin60°=
| ||||
| C、5x2+x-6>0 | ||||
D、sin45°难道不等于
|
函数y=
的值域是 ( )
| x2-8x+15 |
| x2-x-6 |
| A、(-∞,1) | ||||
| B、(-∞,1)∪(1,+∞) | ||||
C、(-∞,-
| ||||
D、(-∞,-
|
 一流的高尔夫选手约70杆即可打完十八洞,而初学者约160杆才可打完十八洞.如图是甲、乙两位高尔夫选手在五次训练测试中打出的杆数的茎叶图,则发挥比较稳定的选手的方差为
一流的高尔夫选手约70杆即可打完十八洞,而初学者约160杆才可打完十八洞.如图是甲、乙两位高尔夫选手在五次训练测试中打出的杆数的茎叶图,则发挥比较稳定的选手的方差为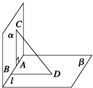 如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,|AC|=6,|AB|=8,|BD|=24,则线段CD的长是( )
如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,|AC|=6,|AB|=8,|BD|=24,则线段CD的长是( )