题目内容
已知Sn=
+
+
+
+…+
,求Sn.
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| 4 |
| 24 |
| n |
| 2n |
考点:数列的求和
专题:等差数列与等比数列
分析:观察所求数列的各项的关系,分母是等比数列,分子是等差数列,求和利用错位相减法.
解答:
解:Sn=
+
+
+
+…+
,…①,
①×
可得:
Sn=
+
+
+
+…+
…②,
①-②得:
Sn=
+
+
+
+…+
-
=
-
.
∴Sn=2-
-
.
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| 4 |
| 24 |
| n |
| 2n |
①×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| 4 |
| 25 |
| n |
| 2n+1 |
①-②得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n+1 |
∴Sn=2-
| 1 |
| 2n-1 |
| n |
| 2n |
点评:本题考查数列求法的基本方法,错位相减法的应用,考查计算能力.

练习册系列答案
相关题目
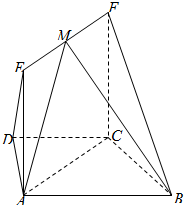 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠CBA=30°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=3.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠CBA=30°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=3.
 正四棱锥S-ABCD中,底面正方形ABCD的边长为a,侧棱长为2a,M为SA中点,N为棱SC中点,求异面直线DM与BN所成角的余弦值.
正四棱锥S-ABCD中,底面正方形ABCD的边长为a,侧棱长为2a,M为SA中点,N为棱SC中点,求异面直线DM与BN所成角的余弦值.