题目内容
已知函数f(x)=|x-2|,g(x)=-|x-3|+m.
(Ⅰ)解不等式f(x)>x+1;
(Ⅱ)若y=f(x)与y=g(x)图象上有公共点,求实数m的取值范围.
(Ⅰ)解不等式f(x)>x+1;
(Ⅱ)若y=f(x)与y=g(x)图象上有公共点,求实数m的取值范围.
考点:绝对值不等式的解法,函数的图象
专题:计算题,不等式的解法及应用
分析:(Ⅰ)运用绝对值的定义,可得
或
,分别解出它们,再求并集即可;
(Ⅱ)y=f(x)与y=g(x)图象上有公共点,即方程f(x)=g(x)有解.即m=|x-2|+|x-3|有解,运用去绝对值的方法求出右边的值域即可.
|
|
(Ⅱ)y=f(x)与y=g(x)图象上有公共点,即方程f(x)=g(x)有解.即m=|x-2|+|x-3|有解,运用去绝对值的方法求出右边的值域即可.
解答:
解:(Ⅰ)不等式f(x)>x+1即为|x-2|>x+1,
即有
或
,即x∈∅或x<
,
故不等式的解集为(-∞,
);
(Ⅱ)y=f(x)与y=g(x)图象上有公共点,即方程f(x)=g(x)有解.
f(x)=g(x)即|x-2|=-|x-3|+m.即有m=|x-2|+|x-3|,
由于y=|x-2|+|x-3|=
,则函数y的值域为[1,+∞).
则m≥1.
故实数m的取值范围是[1,+∞).
即有
|
|
| 1 |
| 2 |
故不等式的解集为(-∞,
| 1 |
| 2 |
(Ⅱ)y=f(x)与y=g(x)图象上有公共点,即方程f(x)=g(x)有解.
f(x)=g(x)即|x-2|=-|x-3|+m.即有m=|x-2|+|x-3|,
由于y=|x-2|+|x-3|=
|
则m≥1.
故实数m的取值范围是[1,+∞).
点评:本题考查绝对值不等式的解法,考查两函数的图象有交点转化为方程有解,考查分离参数法,求含绝对值的函数的值域的方法,属于中档题.

练习册系列答案
相关题目
双曲线
-
=1(b>0)的一条渐近线方程为y=
x,则双曲线的离心率等于( )
| x2 |
| 9 |
| y2 |
| b2 |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
| C、C、 | ||||
D、
|
给出下列定义:
①对于函数f(x),若存在x0∈R使f(x0)=x0成立,则称x0为函数f(x)的不动点;
②若函数的定义域区间与值域区间完全相同,则称该区间为函数的保值区间.
设函数f(x)=x2-2ax+a2+a(x∈R),则该函数有( )
①对于函数f(x),若存在x0∈R使f(x0)=x0成立,则称x0为函数f(x)的不动点;
②若函数的定义域区间与值域区间完全相同,则称该区间为函数的保值区间.
设函数f(x)=x2-2ax+a2+a(x∈R),则该函数有( )
| A、一个不动点和一个保值区间 |
| B、两个不动点和一个保值区间 |
| C、两个不动点和两个保值区间 |
| D、两个不动点和三个保值区间 |
已知实数x,y满足
,则x2+y2+4x+6y+14的最大值为( )
|
| A、42 | ||
B、
| ||
C、
| ||
| D、46 |
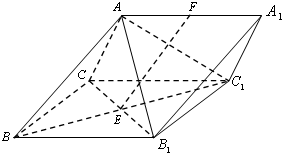 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,BC1与B1C的交点为E,AC=AB1,F为AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,BC1与B1C的交点为E,AC=AB1,F为AA1的中点.