Question

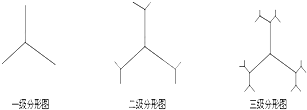某种平面分形图如图所示，一级分形图是由一点出发的三条线段，长度均为1，两两夹角为120°；二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来

1

3

的线段；且这两条线段与原线段两两夹角为120°；…；依此规律得到n级分形图，则
（Ⅰ）四级分形图中共有

 

条线段；
（Ⅱ）n级分形图中所有线段的长度之和为

 

．

Answer 1

考点：数列的求和,数列的函数特性

专题：等差数列与等比数列

分析：（I）当n=1时，共有3条线段；当n=2时，共有3+3×（3-1）=9条线段；当n=3时，共有3+3×（3-1）+3×2²=21条线段；由此规律可得：当n=4时，共有3+3×（3-1）+3×2²+3×2³．
（II）由（I）可得：n级分形图中所有线段的长度之和=3+

1

3

×3×2+

1

32

×3×2²+…+

1

3n-1

×3×2n-1
=3[1+

2

3

+(

2

3

)2+…+(

2

3

)n-1]，利用等比数列的前n项和公式即可得出．

解答： 解：（I）当n=1时，共有3条线段；
当n=2时，共有3+3×（3-1）=9条线段；
当n=3时，共有3+3×（3-1）+3×2²=21条线段；
当n=4时，共有3+3×（3-1）+3×2²+3×2³=45条线段．
（II）由（I）可得：n级分形图中所有线段的长度之和
=3+

1

3

×3×2+

1

32

×3×2²+…+

1

3n-1

×3×2n-1
=3[1+

2

3

+(

2

3

)2+…+(

2

3

)n-1]
=3×

1-( 2 3 )n

1- 2 3

=9[1-(

2

3

)n]．
故答案分别为：45，9[1-(

2

3

)n]．

点评：本题考查了通过观察、方向、猜想、归纳数列通项公式的方法，考查了等比数列的前n项函数公式，考察了推理能力和计算能力，属于难题．