题目内容
方程x2-4x+4=lnx的解的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:根的存在性及根的个数判断
专题:数形结合法,函数的性质及应用
分析:方程x2-4x+4=lnx的解的个数,即为函数y=x2-4x+4与y=lnx的图象交点的个数,在同一坐标系中画出两个函数的图象,可得答案.
解答:
解:方程x2-4x+4=lnx的解的个数,
即为函数y=x2-4x+4与y=lnx的图象交点的个数,
在同一坐标系中画出两个函数的图象如下图所示:

由图可得,两个函数的图象共有2个交点,
故方程x2-4x+4=lnx的解的个数有2个,
故选:B
即为函数y=x2-4x+4与y=lnx的图象交点的个数,
在同一坐标系中画出两个函数的图象如下图所示:

由图可得,两个函数的图象共有2个交点,
故方程x2-4x+4=lnx的解的个数有2个,
故选:B
点评:本题主要考查方程根的个数的判断,构造函数,利用方程和函数之间的关系,即可得到结论.

练习册系列答案
相关题目
函数y=(
)x2-6x+17的值域是( )
| 1 |
| 2 |
| A、R | ||
B、(0,
| ||
C、(-∞,
| ||
D、[
|
在△ABC中,角A,B,C所对的边为a,b,c,满足:sin(A-B)+2cosAsinB=-2sin2C,且16a2+16b2-13c2=0.若△ABC的面积为
,则a+b值为( )
3
| ||
| 4 |
| A、5 | B、6 | C、7 | D、8 |
要得到函数y=-cos2x的图象,可以将y=sin2x的图象( )
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
M={x|0≤x≤2},N={y|0≤y≤3}给出下列四个图形,其中能表示从集合M到集合N的函数关系的有( )


| A、0个 | B、1个 | C、2个 | D、3个 |
若|
|=2,|
|=4且(
+
)⊥
,则
与
的夹角是( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、-
|
若集合M={x|y=2-x},P={x|y=
},则M∩P等于( )
| x-1 |
| A、{x|x>1} |
| B、{x|x≥1} |
| C、{y|y>0} |
| D、{y|y≥0} |
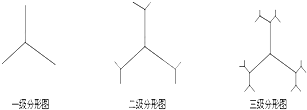 某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来
某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来