题目内容
[81-0.25+(3
) -
] -
+(log43+log83)(log32+log92)= .
| 3 |
| 8 |
| 1 |
| 3 |
| 1 |
| 2 |
考点:对数的运算性质
专题:计算题
分析:化小数为分数,化带分数为假分数,把对数式化为同底数,然后直接利用有理指数幂的运算性质及对数的运算性质化简求值.
解答:
解:[81-0.25+(3
) -
] -
+(log43+log83)(log32+log92)
=[(34)-
+(
)-
]-
+(log23
+log23
)(log32+log32
)
=(
+
)-
+log23
+
•log32•2
=1+
log23•
log32=1+
=
.
故答案为:
.
| 3 |
| 8 |
| 1 |
| 3 |
| 1 |
| 2 |
=[(34)-
| 1 |
| 4 |
| 27 |
| 8 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
=(
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
=1+
| 5 |
| 6 |
| 3 |
| 2 |
| 5 |
| 4 |
| 9 |
| 4 |
故答案为:
| 9 |
| 4 |
点评:本题考查了有理指数幂的运算性质及对数的运算性质,是基础的计算题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
a>1,对任意的x∈[a,2a]都有y∈[a,a2]满足方程logax+logay=3,则a的集合( )
| A、[2,3] |
| B、[2,+∞) |
| C、(1.25,1.75) |
| D、(1.75,2) |
已知函数f(x)=
,则f[f(2013)]=( )
|
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
M={x|0≤x≤2},N={y|0≤y≤3}给出下列四个图形,其中能表示从集合M到集合N的函数关系的有( )


| A、0个 | B、1个 | C、2个 | D、3个 |
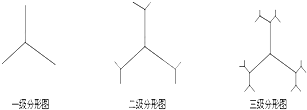 某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来
某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来