题目内容
已知数列{an}满足a1=1,an=
+1,则an= .
| 1 |
| an-1 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由数列递推式结合首项求出前5项,分析得到数列{an}的前两项等于项数,从第三项起,项的分子与分子,分母与分母的差构成等差数列,利用累加法分别求出分子和分母的通项,作比后得答案.
解答:
解:由a1=1,an=
+1,得
a2=
+1=2,
a3=
+1=
+1=
,
a4=
+1=
+1=
,
a5=
+1=
+1=
,
∴数列{an}的前两项等于项数,从第三项起,
项的分子与分子,分母与分母的差构成等差数列,
由累加法求得an=
(n≥3).
∴an=
.
故答案为:
.
| 1 |
| an-1 |
a2=
| 1 |
| a1 |
a3=
| 1 |
| a2 |
| 1 |
| 2 |
| 3 |
| 2 |
a4=
| 1 |
| a3 |
| 2 |
| 3 |
| 5 |
| 3 |
a5=
| 1 |
| a4 |
| 3 |
| 5 |
| 8 |
| 5 |
∴数列{an}的前两项等于项数,从第三项起,
项的分子与分子,分母与分母的差构成等差数列,
由累加法求得an=
| n2-3n+6 |
| n2-5n+10 |
∴an=
|
故答案为:
|
点评:本题考查了数列递推式,训练了累加法求数列的通项公式,关键是对规律的发现,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=(
)x2-6x+17的值域是( )
| 1 |
| 2 |
| A、R | ||
B、(0,
| ||
C、(-∞,
| ||
D、[
|
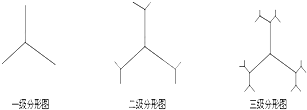 某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来
某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来