题目内容
对于非零向量
,
,下列运算中正确的有( )个.
①
•
=0,则
=0或
=0
②(
•
)•
=
•(
•
)
③|
•
|=|
|•|
|
④
•
=
•
,则
=
.
| a |
| b |
①
| a |
| b |
| a |
| b |
②(
| a |
| b |
| c |
| a |
| b |
| c |
③|
| a |
| b |
| a |
| b |
④
| a |
| c |
| b |
| c |
| a |
| b |
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据数量积的运算及计算公式,数乘的运算,容易判断正确的个数.
解答:
解:①
•
=|
||
|cosθ=0(θ为
,
的夹角);
∴cosθ=0,且
,
是向量,不会为0,∴①错误;
②(
•
)•
中第一个点表示数量积的点乘,第二个点表示数乘的点,所以括号不能移到后两项.∴②错误.
③|
•
|=||
|•|
|cosθ|,θ表示
,
的夹角,只有|cosθ|=1时③才成立,所以该运算不正确.
④由
•
=
•
得:(
-
)•
=|
-
||
|cosθ=0,∴可能cosθ=0,∴不一定得出
=
,∴该运算错误.
故选:A.
| a |
| b |
| a |
| b |
| a |
| b |
∴cosθ=0,且
| a |
| b |
②(
| a |
| b |
| c |
③|
| a |
| b |
| a |
| b |
| a |
| b |
④由
| a |
| c |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
故选:A.
点评:考查数量积的计算公式,向量数量积的运算律,及向量的长度.

练习册系列答案
相关题目
a>1,对任意的x∈[a,2a]都有y∈[a,a2]满足方程logax+logay=3,则a的集合( )
| A、[2,3] |
| B、[2,+∞) |
| C、(1.25,1.75) |
| D、(1.75,2) |
设函数f(x)=
,则下列结论错误的是( )
|
| A、f(x)不是单调函数 |
| B、f(x)不是周期函数 |
| C、f(x)是偶函数 |
| D、f(x)的值域为{0,1} |
已知函数f(x)=
,则f[f(2013)]=( )
|
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
函数y=(
)x2-6x+17的值域是( )
| 1 |
| 2 |
| A、R | ||
B、(0,
| ||
C、(-∞,
| ||
D、[
|
在△ABC中,角A,B,C所对的边为a,b,c,满足:sin(A-B)+2cosAsinB=-2sin2C,且16a2+16b2-13c2=0.若△ABC的面积为
,则a+b值为( )
3
| ||
| 4 |
| A、5 | B、6 | C、7 | D、8 |
若集合M={x|y=2-x},P={x|y=
},则M∩P等于( )
| x-1 |
| A、{x|x>1} |
| B、{x|x≥1} |
| C、{y|y>0} |
| D、{y|y≥0} |
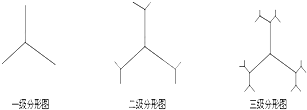 某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来
某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来