题目内容
若a=3 sin60°,b=log
cos60°,c=log2tan30°,则( )
| 1 |
| 3 |
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、b>a>c |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用指数函数和对数函数的性质求解.
解答:
解:∵a=3 sin60°>30=1,
0=log
1<b=log
cos60°<log
=1,
c=log2tan30°<log21=0,
∴a>b>c.
故选:A.
0=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
c=log2tan30°<log21=0,
∴a>b>c.
故选:A.
点评:本题考查三个数大小的比较,是基础题,解题时要注意指数函数、对数函数、三角函数的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
a>1,对任意的x∈[a,2a]都有y∈[a,a2]满足方程logax+logay=3,则a的集合( )
| A、[2,3] |
| B、[2,+∞) |
| C、(1.25,1.75) |
| D、(1.75,2) |
设函数f(x)=
,则下列结论错误的是( )
|
| A、f(x)不是单调函数 |
| B、f(x)不是周期函数 |
| C、f(x)是偶函数 |
| D、f(x)的值域为{0,1} |
函数y=(
)x2-6x+17的值域是( )
| 1 |
| 2 |
| A、R | ||
B、(0,
| ||
C、(-∞,
| ||
D、[
|
若|
|=2,|
|=4且(
+
)⊥
,则
与
的夹角是( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、-
|
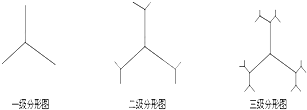 某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来
某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来