题目内容
设Sn是等差数列{an}的前n项和，若
=
，则
（ ）
| S3 |
| S6 |
| 1 |
| 3 |
| S6 |
| S11 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：利用等差数列的前n项和公式求解．
解答：
解：∵Sn是等差数列{an}的前n项和，
=
，
∴
=
=
，
解得a1=2d，
∴
=
=
．
故选：B．
| S3 |
| S6 |
| 1 |
| 3 |
∴
| 3a1+3d |
| 6a1+15d |
| a1+d |
| 2a1+5d |
| 1 |
| 3 |
解得a1=2d，
∴
| S6 |
| S11 |
| 6a1+15d |
| 11a1+55d |
| 27 |
| 77 |
故选：B．
点评：本题考查等差数列的前6项和与前11项和的比的求法，是基础题，解题时要认真审题，注意等差数列的前n项和公式的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x-1）是偶函数，且x＜-1时，f′（x）＞0恒成立，又f（2）=0，则（x+1）f（x+2）＜0的解集为（ ）
| A、（-∞，-2）∪（4，+∞） |
| B、（-6，-1）∪（0，4） |
| C、（-6，-1）∪（0，+∞） |
| D、（-∞，-6）∪（4，+∞） |
如果θ=3rad，那么角θ的终边所在的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
命题“?x＞0，sinx=0”的否定为（ ）
| A、?x＞0，sinx≠0 |
| B、?x≤0，sinx≠0 |
| C、?x≤0，sinx≠0 |
| D、?x＞0，sinx≠0 |
点P（x，y）在直线x+y-2=0上，则P到原点距离的最小值是（ ）
A、2
| ||
B、
| ||
| C、1 | ||
| D、2． |
设直线y=
x与圆C：（x-2）2+y2=4交于A，B两点，则弦长|AB|=（ ）
| 3 |
A、
| ||
B、2
| ||
| C、1 | ||
| D、2 |
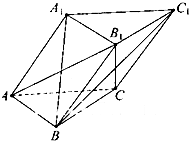已知三棱柱ABC-A1B1C1中，底面边长和侧棱长均为a，侧面A1ACC1⊥底面ABC，A1B=