题目内容
（x+1）（x2+2）＞0是 （x+1）（x+2）＞0的（ ）条件．
| A、必要不充分 |
| B、充要 |
| C、充分不必要 |
| D、既不充分也不必要 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的等价条件求出不等式的解以及充分条件和必要条件的定义即可得到结论．
解答：
解：由（x+1）（x2+2）＞0解得x＞-1，
由（x+1）（x+2）＞0，得x＞-1或x＜-2，
即（x+1）（x2+2）＞0是 （x+1）（x+2）＞0的充分不必要条件，
故选：C
由（x+1）（x+2）＞0，得x＞-1或x＜-2，
即（x+1）（x2+2）＞0是 （x+1）（x+2）＞0的充分不必要条件，
故选：C
点评：本题主要考查充分条件和必要条件的判断，根据不等式的解法是解决本题的关键．
练习册系列答案
相关题目
已知函数f（x）=x3+ax2-3x+c是奇函数．则函数f（x）的单调减区间是（ ）
| A、[-1，1] |
| B、（1，+∞） |
| C、（-∞，1） |
| D、（-∞，+∞） |
已知a=lgx，则a+3等于（ ）
| A、lg（3x） |
| B、lg（3+x） |
| C、lgx3 |
| D、lg（1000x） |
已知直线a、b、c及平面α，它们具备下列哪组条件时，有b∥c成立（ ）
| A、b⊥a且c⊥a |
| B、b⊥α且c⊥α |
| C、b、c和α所成的角相等 |
| D、b∥α且c∥α |
下列图形中不一定是平面图形的是（ ）
| A、三角形 |
| B、梯形 |
| C、两组对边分别相等的四边形 |
| D、两组对边分别平行的四边形 |
已知平行四边形ABCD的顶点A（3，-1）、C（2，-3），点D在直线3x-y+1=0上移动，则点B的轨迹方程为（ ）
| A、3x-y-20=0（x≠3） |
| B、3x-y-10=0（x≠3） |
| C、3x-y-9=0（x≠2） |
| D、3x-y-12=0（x≠5） |
曲线y=x3-x+3在点（1，3）处的切线的斜率等于（ ）
| A、2 | B、4 | C、12 | D、6 |
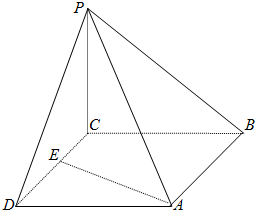如图，四棱锥P-ABCD的底面为正方形，平面PCD⊥平面ABCD，平面PBC⊥平面ABCD，E为线段CD上任意一点（不包括端点）．