题目内容
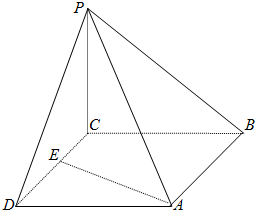如图，四棱锥P-ABCD的底面为正方形，平面PCD⊥平面ABCD，平面PBC⊥平面ABCD，E为线段CD上任意一点（不包括端点）．（Ⅰ）求证：PC⊥平面ABCD；
（Ⅱ）若∠PBC=
| π |
| 4 |
（Ⅲ）在线段PA上是否存在点H，使得EH∥平面PBC？如果存在，找出点H；如果不存在，请说明理由．
考点：二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定
专题：作图题,证明题,空间位置关系与距离
分析：（1）由四边形ABCD正方形可知BC⊥CD，从而可证明BC⊥平面PCD，进而证明BC⊥PC，再证CD⊥PC，由线面垂直判定定理可证明PC⊥平面ABCD．（2）作CF⊥AE，交AE的延长线与点F，连接PF．则∠PFC为二面角P-AE-B的平面角；通过解三角形求正切值；（3）在平面ABCD内，过点E作EM∥BC交AB于点M，在平面PAB内，过点M作MH∥PB交PA于点H，点H即为所作点．
解答：
解：（Ⅰ）证明：∵四边形ABCD为正方形，∴BC⊥CD，
又∵平面PCD⊥平面ABCD，平面PCD∩平面ABCD=CD，
∴BC⊥平面PCD，而PC⊆平面PCD，∴BC⊥PC，
同理可证：CD⊥PC，
又CD∩BC=C，且CD，BC⊆平面ABCD，
∴PC⊥平面ABCD．
（Ⅱ）作CF⊥AE，交AE的延长线与点F，连接PF．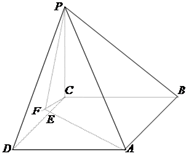
∵AE⊆平面ABCD，由（Ⅰ）知PC⊥AE，又CF⊥AE，且CF∩PC=C，
∴AE⊥平面PCF，
∵PF⊆平面PCF，∴PF⊥AE，
即∠PFC为二面角P-AE-B的平面角．
设正方形ABCD的边长为2a，则CE=a，则AE=
a，
而∠CEF=∠AED，∠ADE=∠CFE=
，
∴△AED∽△CEF，
∴
=
，则CF=
=
a，
∵BC⊥PC，∠PBC=
，∴PC=2a，
故tan∠PFC=
=
=
．
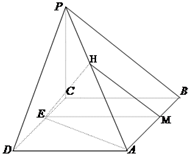
（Ⅲ）在平面ABCD内，过点E作EM∥BC交AB于点M，
在平面PAB内，过点M作MH∥PB交PA于点H，点H即为所作点，证明如下：
∵EM∥BC，EM?平面PBC，BC⊆平面PBC，
∴EM∥平面PBC，同理可证MH∥平面PBC，
又∵EM∩MH=M，EM，MH⊆平面EMH，
∴平面EMH∥平面PBC，而EH⊆平面EMH，
∴EH∥平面PBC，
故在线段PA上存在点H，使得EH∥面PBC．
又∵平面PCD⊥平面ABCD，平面PCD∩平面ABCD=CD，
∴BC⊥平面PCD，而PC⊆平面PCD，∴BC⊥PC，
同理可证：CD⊥PC，
又CD∩BC=C，且CD，BC⊆平面ABCD，
∴PC⊥平面ABCD．
（Ⅱ）作CF⊥AE，交AE的延长线与点F，连接PF．
∵AE⊆平面ABCD，由（Ⅰ）知PC⊥AE，又CF⊥AE，且CF∩PC=C，
∴AE⊥平面PCF，
∵PF⊆平面PCF，∴PF⊥AE，
即∠PFC为二面角P-AE-B的平面角．
设正方形ABCD的边长为2a，则CE=a，则AE=
| 5 |
而∠CEF=∠AED，∠ADE=∠CFE=
| π |
| 2 |
∴△AED∽△CEF，
∴
| CF |
| AD |
| CE |
| AE |
| a•2a | ||
|
2
| ||
| 5 |
∵BC⊥PC，∠PBC=
| π |
| 4 |
故tan∠PFC=
| PC |
| CF |
| 2a | ||||
|
| 5 |
（Ⅲ）在平面ABCD内，过点E作EM∥BC交AB于点M，
在平面PAB内，过点M作MH∥PB交PA于点H，点H即为所作点，证明如下：
∵EM∥BC，EM?平面PBC，BC⊆平面PBC，
∴EM∥平面PBC，同理可证MH∥平面PBC，
又∵EM∩MH=M，EM，MH⊆平面EMH，
∴平面EMH∥平面PBC，而EH⊆平面EMH，
∴EH∥平面PBC，
故在线段PA上存在点H，使得EH∥面PBC．
点评：本题综合性较强，考查了面面垂直的性质定理，线面垂直判定定理，二面角的平面角的作法等，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（x+1）（x2+2）＞0是 （x+1）（x+2）＞0的（ ）条件．
| A、必要不充分 |
| B、充要 |
| C、充分不必要 |
| D、既不充分也不必要 |
