题目内容
现有数列{an}满足：a1=1，且对任意的m，n∈N*都有：am+n=am+an+mn，则
+
+
+…+
=
（ ）
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2014 |
（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：数列的求和
专题：等差数列与等比数列
分析：令m=1，得an+1-an=1+n，由此利用累加法求出an=
．从而得到
=2（
-
），由此利用裂项求和法能求出
+
+
+…+
．
| n(n+1) |
| 2 |
| 1 |
| an |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2014 |
解答：
解：∵数列{an}满足：a1=1，
且对任意的m，n∈N*都有：am+n=am+an+mn，
∴令m=1，得an+1=an+a1+n，
∴an+1-an=1+n，
∴an=a1+（a2-a1）+…+（an-an-1）=1+2+…+n=
．
∴
=
=2（
-
），
∴
+
+
+…+
=2（1-
+
-
+
-
+…+
-
）=2（1-
）=
．
故选：D．
且对任意的m，n∈N*都有：am+n=am+an+mn，
∴令m=1，得an+1=an+a1+n，
∴an+1-an=1+n，
∴an=a1+（a2-a1）+…+（an-an-1）=1+2+…+n=
| n(n+1) |
| 2 |
∴
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2014 |
=2（1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2014 |
| 1 |
| 2015 |
| 1 |
| 2015 |
| 4028 |
| 2015 |
故选：D．
点评：本题考查数列的前n项和的求法，是中档题，解题时要认真审题，注意裂项求和法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
设a，b是两条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是（ ）
| A、若α⊥β，α⊥γ，则β⊥γ |
| B、若a，b与α所成的角相等，则a∥b |
| C、若a⊥α，a∥β，则α⊥β |
| D、若a∥b，a?α，则b∥α |
直线l的方向向量与平面α的法向量的夹角为150°，则l与平面α所成的角为（ ）
| A、120° | B、30° |
| C、60° | D、150° |
已知n是正偶数，用数学归纳法证明某命题时，若已假设n=k（k≥2且为偶数）时命题为真，则还需证明（ ）
| A、n=k+1时命题成立 |
| B、n=k+2时命题成立 |
| C、n=2k+2时命题成立 |
| D、n=2（k+2）时命题成立 |
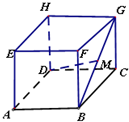如图，正方体ABCD-EFGH中，M为BG的中点，则直线DM与平面ABCD所成角的正切值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
没有信息损失的统计图表是（ ）
| A、条形统计图 | B、扇形统计图 |
| C、折线统计图 | D、茎叶图 |
