题目内容
函数y=cosx•ln|x|的部分图象大致是下图中的（ ）
A、 |
B、 |
C、 |
D、 |
考点：抽象函数及其应用
专题：函数的性质及应用
分析：根据函数的定义域和奇偶性判断即可．
解答：
∵y=cosx是偶函数，y=ln|x|是偶函数，且x≠0，∴y=cosx•ln|x|是定义域为{x∈R|x≠0}的偶函数．
∴排除C、D，又∵当x去非常小的正数时，cosx＞0，ln|x|＜0，∴y＜0，∴排除A故选B
故选B
∴排除C、D，又∵当x去非常小的正数时，cosx＞0，ln|x|＜0，∴y＜0，∴排除A故选B
故选B
点评：抽像函数的图象可以通过定义域、值域、单调性、奇偶性以及特殊值进行排除．一般不需要直接列表描点作图．
练习册系列答案
相关题目
点P是椭圆
+
=1上一点，F1，F2为椭圆两焦点，若∠F1PF2=90°，则△PF1F2面积为（ ）
| x2 |
| 100 |
| y2 |
| 64 |
| A、64 | ||||
| B、36 | ||||
C、36(2-
| ||||
D、
|
| 1-sin2100° |
| A、cos100° |
| B、±cos100° |
| C、±cos80° |
| D、cos80° |
函数y=
的图象与函数y=2cos2
x（-3≤x≤5）的图象所有交点的纵坐标之和等于（ ）
| x |
| x-1 |
| π |
| 4 |
| A、2 | B、4 | C、6 | D、8 |
设a，b是两条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是（ ）
| A、若α⊥β，α⊥γ，则β⊥γ |
| B、若a，b与α所成的角相等，则a∥b |
| C、若a⊥α，a∥β，则α⊥β |
| D、若a∥b，a?α，则b∥α |
“|x|≥1”是“x≥1”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
在极坐标系中，曲线ρ（cosθ+sinθ）=1，则曲线在直角坐标系中方程为（ ）
| A、x+y=2 | B、x-y=1 |
| C、x=1 | D、x+y=1 |
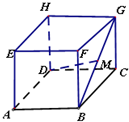如图，正方体ABCD-EFGH中，M为BG的中点，则直线DM与平面ABCD所成角的正切值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|