题目内容
已知双曲线
-
=1的一条渐近线方程为4x+3y=0,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意双曲线
-
=1的一条渐近线方程为4x+3y=0,可得b:a=4:3,结合双曲线的平方关系可得c与a的比值,求出该双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:∵双曲线
-
=1的一条渐近线方程为4x+3y=0,
∴b=
a,
∴c=
=
a,
∴e=
=
.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
∴b=
| 4 |
| 3 |
∴c=
| a2+b2 |
| 5 |
| 3 |
∴e=
| c |
| a |
| 5 |
| 3 |
故选:A.
点评:本题考查双曲线的离心率的求法,解题时要认真审题,要熟练掌握双曲线的离心率、渐近线方程等基础知识.

练习册系列答案
相关题目
函数y=
的图象与函数y=2cos2
x(-3≤x≤5)的图象所有交点的纵坐标之和等于( )
| x |
| x-1 |
| π |
| 4 |
| A、2 | B、4 | C、6 | D、8 |
正三棱锥的高是
,侧棱长为
,那么侧面与底面所成的二面角是( )
| 3 |
| 7 |
| A、60° | B、30° |
| C、45° | D、75° |
某人朝正东方走xkm后,向左转150°,然后朝新方向走3km,结果它离出发点恰好
km,那么x等于( )
| 3 |
A、
| ||||
B、2
| ||||
C、
| ||||
| D、3 |
在棱长为3的正方体内任取一个点,则这个点到各面的距离大于1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
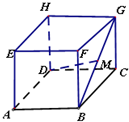 如图,正方体ABCD-EFGH中,M为BG的中点,则直线DM与平面ABCD所成角的正切值为( )
如图,正方体ABCD-EFGH中,M为BG的中点,则直线DM与平面ABCD所成角的正切值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图所示是函数f(x)的导函数f′(x)的图象,则下列判断中正确的是( )


| A、函数f(x)在区间(-2,0)上是减函数 |
| B、函数f(x)在区间(1,3)上是减函数 |
| C、函数f(x)在区间(0,2)上是减函数 |
| D、函数f(x)在区间(3,4)上是增函数 |
 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.