题目内容
已知点A(4,0),B(1,0),若动点T满足
•
=6|
|.
(1)求动点T的轨迹Γ;
(2)在x轴正半轴上是否存在一点P,过该点的直线l(不与x轴重合)与曲线Γ交于两点M,N,使得
+
为定值,若有求出P点坐标和定值,若不存在,说明理由.
| AB |
| AT |
| BT |
(1)求动点T的轨迹Γ;
(2)在x轴正半轴上是否存在一点P,过该点的直线l(不与x轴重合)与曲线Γ交于两点M,N,使得
| 1 |
| |PM|2 |
| 1 |
| |PN|2 |
考点:轨迹方程,平面向量数量积的运算
专题:向量与圆锥曲线
分析:(1)设出动点坐标,得到向量
,
,
的坐标,代入
•
=6|
|整理得到动点T的轨迹Γ;
(2)假设存在定点P(m,0)(m>0),使得
+
为定值,设出M,N的坐标及直线l的方程x=ty+m,
把
+
用M,N的坐标及t表示,再把直线和椭圆方程联立后利用根与系数关系得到M,N的纵坐标的关系,代入
+
整理得到关于m的表达式,然后由分子的系数关系求得m的值,则答案可求.
| AT |
| AB |
| BT |
| AB |
| AT |
| BT |
(2)假设存在定点P(m,0)(m>0),使得
| 1 |
| |PM|2 |
| 1 |
| |PN|2 |
把
| 1 |
| |PM|2 |
| 1 |
| |PN|2 |
| 1 |
| |PM|2 |
| 1 |
| |PN|2 |
解答:
解:(1)设动点T(x,y),
∵A(4,0),B(1,0),
∴
=(x-4,y),
=(-3,0),
=(x-1,y),
代入
•
=6|
|,整理得:
+
=1;
(2)假设存在定点P(m,0)(m>0),使得
+
为定值.
设M(x1,y1),N(x2,y2),直线l:x=ty+m,
则|PM|2=(x1-m)2+y12=(t2+1)y12,|PN|2=(t2+1)y22.
∴
+
=
(
+
)=
=
(1)
联立x=ty+m与
+
=1,整理得:(3t2+4)y2+6tmy+3m2-12=0.
∴y1+y2=
,y1y2=
,代入(1)式得:
.
要使得上式为定值,须18m2+72=96-24m2,解得m=
,
此时
+
取到定值
.
∴当P为(
,0)时,
+
取到定值
.
∵A(4,0),B(1,0),
∴
| AT |
| AB |
| BT |
代入
| AB |
| AT |
| BT |
| x2 |
| 4 |
| y2 |
| 3 |
(2)假设存在定点P(m,0)(m>0),使得
| 1 |
| |PM|2 |
| 1 |
| |PN|2 |
设M(x1,y1),N(x2,y2),直线l:x=ty+m,
则|PM|2=(x1-m)2+y12=(t2+1)y12,|PN|2=(t2+1)y22.
∴
| 1 |
| |PM|2 |
| 1 |
| |PN|2 |
| 1 |
| (t2+1) |
| 1 |
| y12 |
| 1 |
| y22 |
| 1 |
| (t2+1) |
| y12+y22 |
| y12y22 |
=
| 1 |
| (t2+1) |
| (y1+y2)2-2y1y2 |
| y12y22 |
联立x=ty+m与
| x2 |
| 4 |
| y2 |
| 3 |
∴y1+y2=
| -6tm |
| 3t2+4 |
| 3m2-12 |
| 3t2+4 |
|
要使得上式为定值,须18m2+72=96-24m2,解得m=
2
| ||
| 7 |
此时
| 1 |
| |PM|2 |
| 1 |
| |PN|2 |
| 7 |
| 9 |
∴当P为(
2
| ||
| 7 |
| 1 |
| |PM|2 |
| 1 |
| |PN|2 |
| 7 |
| 9 |
点评:本题考查轨迹方程,考查了向量在解题中的应用,体现了设而不求的解题思想方法,考查了学生的综合运算能力,是压轴题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知全集U=Z,A={-3,1,2},B={1,2,3},则A∩∁UB为( )
| A、{-3,1} |
| B、{1,2} |
| C、{-3} |
| D、{-3,2} |
执行如图所示的一个程序框图,若f(x)在[-1,a]上的值域为[0,2],则实数a的取值范围是( )


| A、(0,1] | ||
B、[1,
| ||
| C、[1,2] | ||
D、[
|
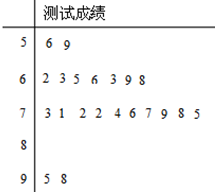 某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下:
某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下: