题目内容
若x，y∈R，xy≠0且x2+my2=mxy，则实数m的取值范围是 ．
考点：基本不等式
专题：不等式的解法及应用
分析：由已知变形利用二次函数的单调性即可得出．
解答：
解：∵x，y∈R，xy≠0且x2+my2=mxy，
∴m=
=
=
，
当分母大于0时，m≥4；当分母小于0时，m＜0．
综上可得：m的取值范围是（-∞，0）∪[4，+∞）．
故答案为：（-∞，0）∪[4，+∞）．
∴m=
| x2 |
| xy-y2 |
| 1 | ||||
-(
|
| 1 | ||||||
-(
|
当分母大于0时，m≥4；当分母小于0时，m＜0．
综上可得：m的取值范围是（-∞，0）∪[4，+∞）．
故答案为：（-∞，0）∪[4，+∞）．
点评：本题考查了二次函数的单调性、不等式的基本性质，属于中档题．
练习册系列答案
相关题目
设集合M={（x，y）|y=2-x}，N={x|y=x}，则M∩N=（ ）
| A、{1，1} | B、{（1，1）} |
| C、{1} | D、∅ |
若直线y=kx与圆（x-1）2+y2=1的两个交点关于直线x-y+b=0对称，则k，b的值分别为（ ）
| A、k=-1，b=1 |
| B、k=-1，b=-1 |
| C、k=1，b=1 |
| D、k=1，b=-1 |
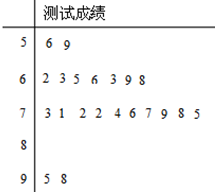某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下：