题目内容
在△ABC中,若(
+
)•
=
|
|2,则
= .
| CA |
| CB |
| AB |
| 3 |
| 5 |
| AB |
| tanA |
| tanB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积运算、正弦定理、和差化积、同角三角函数的基本关系式即可得出.
解答:
解:∵
=
-
,(
+
)•
=
|
|2,
∴(
+
)•(
-
)=
|
|2,
∴
2-
2=
|
|2,
∴a2-b2=
c2,
由正弦定理可得:sin2A-sin2B=
sin2C,
∴
-
=
sin2C,
即
(cos2B-cos2A)=
sin2C,
∴-sin(B+A)sin(B-A)=
sin2C,
∴5sin(A-B)=3sin(A+B),
∴5(sinAcosB-cosAsinB)=3(sinAcosB+cosAsinB),
∴sinAcosB=4cosAsinB,
∴tanA=4tanB,
∴
=4.
故答案为:4.
| AB |
| CB |
| CA |
| CA |
| CB |
| AB |
| 3 |
| 5 |
| AB |
∴(
| CA |
| CB |
| CB |
| CA |
| 3 |
| 5 |
| AB |
∴
| CB |
| CA |
| 3 |
| 5 |
| A B |
∴a2-b2=
| 3 |
| 5 |
由正弦定理可得:sin2A-sin2B=
| 3 |
| 5 |
∴
| 1-cos2A |
| 2 |
| 1-cos2B |
| 2 |
| 3 |
| 5 |
即
| 1 |
| 2 |
| 3 |
| 5 |
∴-sin(B+A)sin(B-A)=
| 3 |
| 5 |
∴5sin(A-B)=3sin(A+B),
∴5(sinAcosB-cosAsinB)=3(sinAcosB+cosAsinB),
∴sinAcosB=4cosAsinB,
∴tanA=4tanB,
∴
| tanA |
| tanB |
故答案为:4.
点评:本题考查了数量积运算、正弦定理、和差化积、同角三角函数的基本关系式,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
执行如图所示的一个程序框图,若f(x)在[-1,a]上的值域为[0,2],则实数a的取值范围是( )


| A、(0,1] | ||
B、[1,
| ||
| C、[1,2] | ||
D、[
|
(4x-2-x)6(x∈R)的展开式中常数项是( )
| A、-20 | B、-15 |
| C、15 | D、20 |
复数z为纯虚数,若(2-i)z=a+i(i为虚数单位),则实数a的值为( )
A、-
| ||
| B、2 | ||
| C、-2 | ||
D、
|
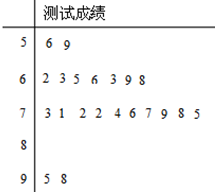 某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下:
某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下: