题目内容
若loga
<1,则a的取值范围是 .
| 12 |
| a-1 |
考点:对数的运算性质
专题:函数的性质及应用
分析:根据对数的性质,先求出a>1,然后根据对数函数的单调性,解不等式即可.
解答:
解:要使对数有意义,则
>0,即a>1,
∴不等式等价为
<a,
即12<a(a-1),
即a2-a-12>0,
即a>4或a<-3,
∵a>1,
∴a>4,
故答案为:(4,+∞).
| 12 |
| a-1 |
∴不等式等价为
| 12 |
| a-1 |
即12<a(a-1),
即a2-a-12>0,
即a>4或a<-3,
∵a>1,
∴a>4,
故答案为:(4,+∞).
点评:本题主要考查对数不等式的解法,利用对数函数的性质是解决本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
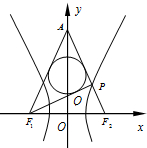 如图,已知双曲线
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
已知l,m是两条不同的直线,α是一个平面,且l∥α,则下列命题正确的是( )
| A、若l∥m,则m∥α |
| B、若m∥α,则l∥m |
| C、若l⊥m,则m⊥α |
| D、若m⊥α,则l⊥m |
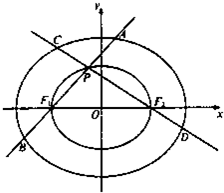 已知椭圆
已知椭圆
 在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈(
在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈(