题目内容
已知函数φ(x)=1n(x+1)+mx,函数f(x)=
(x≥1).
(Ⅰ)若x=0时,函数φ(x)取得极大值,求实数m的值;
(Ⅱ)若f(x)≥
恒成立,求实数k的取值范围;
(Ⅲ)若规定n!=1•2•3…(n-1)•n,求证:2ln[(n+1)!]>1n(n+1)+n-2(n∈N*).
| 1+1nx |
| x |
(Ⅰ)若x=0时,函数φ(x)取得极大值,求实数m的值;
(Ⅱ)若f(x)≥
| k |
| x+1 |
(Ⅲ)若规定n!=1•2•3…(n-1)•n,求证:2ln[(n+1)!]>1n(n+1)+n-2(n∈N*).
考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:计算题,证明题,导数的综合应用
分析:(Ⅰ)求导φ′(x)=
+m,代入求实数m的值,并检验;
(Ⅱ)不等式f(x)≥
可化为k≤
;令g(x)=
,化恒成立问题为最值问题;
(Ⅲ)由(Ⅱ)知,f(x)≥
恒成立,即lnx≥
>1-
;令x=n(n+1),则lnn(n+1)>1-
;从而证明.
| 1 |
| x+1 |
(Ⅱ)不等式f(x)≥
| k |
| x+1 |
| (x+1)(1+lnx) |
| x |
| (x+1)(1+lnx) |
| x |
(Ⅲ)由(Ⅱ)知,f(x)≥
| 2 |
| x+1 |
| x-1 |
| x+1 |
| 2 |
| x |
| 2 |
| n(n+1) |
解答:
解:(Ⅰ)φ′(x)=
+m,
由φ′(0)=1+m=0解得,m=-1;
经检验,函数φ(x)在x=0处取得极大值.
(Ⅱ)不等式f(x)≥
可化为
k≤
;
令g(x)=
,
则g′(x)=
;
令h(x)=x-lnx;
则h′(x)=1-
;
故h(x)在[1,+∞)上递增,
则h(x)≥h(1)=1>0;
则g(x)在[1,+∞)上递增,
故g(x)≥g(1)=2;
故k≤2;
(Ⅲ)证明:由(Ⅱ)知,f(x)≥
恒成立,
即lnx≥
>1-
;
令x=n(n+1),则lnn(n+1)>1-
;
则ln(1×2)>1-
,ln(2×3)>1-
,…,lnn(n+1)>1-
;
叠加得,2lnn!+ln(n+1)>n-2;
2ln[(n+1)!]>1n(n+1)+n-2(n∈N*).
| 1 |
| x+1 |
由φ′(0)=1+m=0解得,m=-1;
经检验,函数φ(x)在x=0处取得极大值.
(Ⅱ)不等式f(x)≥
| k |
| x+1 |
k≤
| (x+1)(1+lnx) |
| x |
令g(x)=
| (x+1)(1+lnx) |
| x |
则g′(x)=
| x-lnx |
| x2 |
令h(x)=x-lnx;
则h′(x)=1-
| 1 |
| x |
故h(x)在[1,+∞)上递增,
则h(x)≥h(1)=1>0;
则g(x)在[1,+∞)上递增,
故g(x)≥g(1)=2;
故k≤2;
(Ⅲ)证明:由(Ⅱ)知,f(x)≥
| 2 |
| x+1 |
即lnx≥
| x-1 |
| x+1 |
| 2 |
| x |
令x=n(n+1),则lnn(n+1)>1-
| 2 |
| n(n+1) |
则ln(1×2)>1-
| 2 |
| 1×2 |
| 2 |
| 2×3 |
| 2 |
| n(n+1) |
叠加得,2lnn!+ln(n+1)>n-2;
2ln[(n+1)!]>1n(n+1)+n-2(n∈N*).
点评:本题考查了导数的综合应用及不等式的证明及恒成立问题,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系xOy中,已知
、
是互相垂直的两个单位向量,点Q满足
=3
+4
.曲线C={P|
=2
cosθ+2
sinθ,0≤θ≤2π},区域Ω={P|0<r≤|
|≤R,r<R}.若C∩Ω=C,则( )
| a |
| b |
| OQ |
| a |
| b |
| OP |
| a |
| b |
| PQ |
| A、0<r≤3且R≥7 |
| B、0<r≤3≤R≤7 |
| C、0<r≤5<R<7 |
| D、5≤r<7≤R |
若(2+2i)(1-mi)(i为虚数单位)为纯虚数,则实数m的值等于( )
| A、1 | B、-1 | C、0 | D、1或-1 |
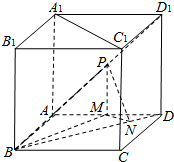 如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.