题目内容
在平面直角坐标系xOy中，已知
、
是互相垂直的两个单位向量，点Q满足
=3
+4
．曲线C={P|
=2
cosθ+2
sinθ，0≤θ≤2π}，区域Ω={P|0＜r≤|
|≤R，r＜R}．若C∩Ω=C，则（ ）
| a |
| b |
| OQ |
| a |
| b |
| OP |
| a |
| b |
| PQ |
| A、0＜r≤3且R≥7 |
| B、0＜r≤3≤R≤7 |
| C、0＜r≤5＜R＜7 |
| D、5≤r＜7≤R |
考点：平面向量的综合题
专题：综合题,平面向量及应用
分析：确定Q（3，4），曲线C={（x，y）|x2+y2=4}，可得3≤|
|≤7，根据C∩Ω=C，即可得出结论．
| PQ |
解答：
解：∵
、
是互相垂直的两个单位向量，点Q满足
=3
+4
，
∴Q（3，4），∴|OQ|=5．
∵曲线C={P|
=2
cosθ+2
sinθ，0≤θ≤2π}，
∴曲线C={（x，y）|x2+y2=4}，
∴3≤|
|≤7，
∵C∩Ω=C，
∴0＜r≤3且R≥7，
故选：A．
| a |
| b |
| OQ |
| a |
| b |
∴Q（3，4），∴|OQ|=5．
∵曲线C={P|
| OP |
| a |
| b |
∴曲线C={（x，y）|x2+y2=4}，
∴3≤|
| PQ |
∵C∩Ω=C，
∴0＜r≤3且R≥7，
故选：A．
点评：本题考查平面向量的综合，考查圆的知识，考查学生分析解决问题的能力，确定3≤|
|≤7是关键．
| PQ |
练习册系列答案
高中必刷题系列答案
相关题目
已知p：方程
+
=1所表示的曲线为焦点在x轴上的椭圆，q：|t-a|＜2（a∈N），若p是q的充分不必要条件，则a取值范围为（ ）
| x2 |
| 3-t |
| y2 |
| t+1 |
| A、（-∞，1] |
| B、[-1，1] |
| C、[0，+∞） |
| D、（0，1） |
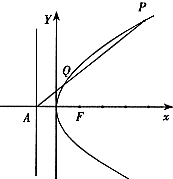抛物线的顶点在原点，焦点在x轴上，准线l与x轴相交于点A（-1，0），过点A的直线与抛物线相交于P、Q两点． 
某海岛上有一座海拔1千米的山，山顶上有一观察站P（P在海平面上的射影点为A），测得一游艇在海岛南偏西30°，俯角为45°的B处，该游艇准备前往海岛正东方向，俯角为45°的旅游景点C处，如图所示．