题目内容
10.把双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的实轴变虚轴,虚轴变实轴,那么所得的双曲线方程为( )| A. | -$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 | B. | -$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | D. | 以上都不对 |
分析 求得双曲线的a=3,b=2,判断所求双曲线焦点在y轴上,把原来的1换为-1,即可得到.
解答 解:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的a=3,b=2,
把双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的实轴变虚轴,虚轴变实轴,
可得所求双曲线方程为$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1.
故选:A.
点评 本题考查双曲线的方程的求法,注意运用方程思想,属于基础题.

练习册系列答案
相关题目
18.设$a=\sqrt{3},b=\sqrt{15}-\sqrt{7},c=\sqrt{11}-\sqrt{3}$,那么a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
15.已知A={x|x≥k},B={x|$\frac{3}{x+1}$<1},若“x∈A”是“x∈B”的充分不必要条件,则k的取值范围是( )
| A. | k<-1 | B. | k≤-1 | C. | k>2 | D. | k≥2 |
2.已知等边△ABC的边长为2$\sqrt{3}$,动点P、M满足|$\overrightarrow{AP}$|=1,$\overrightarrow{PM}$=$\overrightarrow{MC}$,则|$\overrightarrow{BM}$|2的最小值是( )
| A. | $\frac{25}{4}$ | B. | $\frac{31}{4}$ | C. | $\frac{37-6\sqrt{3}}{4}$ | D. | $\frac{37-2\sqrt{33}}{4}$ |
20.下列四组函数中,表示相等函数的一组是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=|x|,g(t)=$\sqrt{{t}^{2}}$ | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=lg(x+1)+lg(x-1),g(x)=lg(x2-1) |
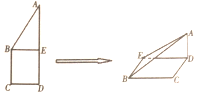 如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述: