题目内容
1.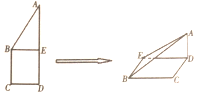 如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:①AB与DE所成角的正切值为$\sqrt{2}$;
②AB∥CE;
③${V_{B-ACE}}=\frac{1}{12}{a^3}$;
④平面ABC⊥平面ADC.其中正确的命题序号为①④.
分析 在①中,由BC∥DE,知∠ABC(或其补角)为AB与DE所成角,由此能求出AB与DE所成角的正切值为$\sqrt{2}$;在②中,由翻折后的图形知AB与CE是异面直线;在③中,VB-ACE=$\frac{1}{6}{a}^{3}$;在④中,由AD⊥平面BCDE,知AD⊥BC,又BC⊥CD,由此推导出平面ABC⊥平面ADC.
解答 解:∵正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,
折起后A点在平面BCDE上的射影为D点,
∴$AB=\sqrt{3}BC$=$\sqrt{3}a$,AE=$\sqrt{2}a$,AD⊥平面BCDE,AD=a,AC=$\sqrt{2}a$,
在①中,∵BC∥DE,∴∠ABC(或其补角)为AB与DE所成角,
∵AB=$\sqrt{3}a$,BC=a,AC=$\sqrt{2}a$,∴BC⊥AC,
∴tan∠ABC=$\sqrt{2}$,∴AB与DE所成角的正切值为$\sqrt{2}$,故①正确;
在②中,由翻折后的图形知AB与CE是异面直线,故②错误;
在③中,${V}_{B_ACE}=\frac{1}{3}{S}_{△BCE}×AD=\frac{1}{3}×\frac{1}{2}{a}^{3}$=$\frac{1}{6}{a}^{3}$,故③错误;
在④中,∵AD⊥平面BCDE,BC?平面ABC,
∴AD⊥BC,又BC⊥CD,AD∩CD=D,
∴BC?平面ADC,又BC?平面ABC,
∴平面ABC⊥平面ADC,故④正确.
故答案为:①④.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
16.已知集合A={x|-1<x<2},B={x|0<x<3},则A∪B等于( )
| A. | (0,2) | B. | (2,3) | C. | (-1,3) | D. | (-1,0) |
6.2016年9 月4日至5日在中国杭州召开了G20峰会,会后某10国集团领导人站成前排3人后排7人准备请摄影师给他们拍照,现摄影师打算从后排7人中任意抽2人调整到前排,使每排各5人.若调整过程中另外8人的前后左右相对顺序不变,则不同调整方法的总数是( )
| A. | $C_7^2A_3^2$ | B. | $C_7^2A_5^5$ | C. | $C_7^2A_5^2$ | D. | $C_7^2A_4^2$ |
10.把双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的实轴变虚轴,虚轴变实轴,那么所得的双曲线方程为( )
| A. | -$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 | B. | -$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | D. | 以上都不对 |