题目内容
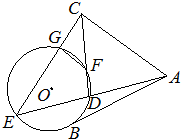 如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.(Ⅰ)证明:AC2=AD•AE;
(Ⅱ)证明:FG∥AC.
考点:与圆有关的比例线段,圆內接多边形的性质与判定
专题:选作题,立体几何
分析:(Ⅰ)利用切线长与割线长的关系及AB=AC进行证明.
(Ⅱ)利用成比例的线段证明角相等、三角形相似,得到同位角角相等,从而两直线平行.
(Ⅱ)利用成比例的线段证明角相等、三角形相似,得到同位角角相等,从而两直线平行.
解答:
证明:(Ⅱ)∵AB是⊙O的一条切线,切点为B,ADE,CFD,CGE都是⊙O的割线,
∴AB2=AD•AE,
∵AB=AC,
∴AD•AE=AC2.
(Ⅱ)由(Ⅱ)有
=
,
∵∠EAC=∠DAC,
∴△ADC∽△ACE,
∴∠ADC=∠ACE,
∵圆的内接四边形对角互补,
∴∠ADC=∠EGF,
∴∠EGF=∠ACE,
∴FG∥AC.
∴AB2=AD•AE,
∵AB=AC,
∴AD•AE=AC2.
(Ⅱ)由(Ⅱ)有
| AD |
| AC |
| AC |
| AE |
∵∠EAC=∠DAC,
∴△ADC∽△ACE,
∴∠ADC=∠ACE,
∵圆的内接四边形对角互补,
∴∠ADC=∠EGF,
∴∠EGF=∠ACE,
∴FG∥AC.
点评:本题考查圆的切线、割线长的关系,平面的基本性质.解决这类问题的常用方法是利用成比例的线段证明角相等、三角形相似等知识.

练习册系列答案
相关题目
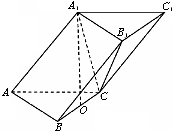 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=