题目内容
已知圆锥的体积是12πcm3,其侧面展开图是中心角为216°的扇形.
(1)求圆锥侧面积;
(2)若一个圆柱下底面在圆锥的底面上,上底面与圆锥面相切,求该圆柱侧面积最大值.
(1)求圆锥侧面积;
(2)若一个圆柱下底面在圆锥的底面上,上底面与圆锥面相切,求该圆柱侧面积最大值.
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:(1)设出圆锥的底面半径以及弧长,通过圆锥的体积是12πcm3,其侧面展开图是中心角为216°列出关系式,求出底面半径以及弧长,即可求解圆锥侧面积.
(2)设内接圆柱的底面半径为r′,高为h′,根据三角形相似找出h′与r′的关系,然后表示出内接圆柱侧面积,最后利用基本不等式求出最值即可,注意等号成立的条件.
(2)设内接圆柱的底面半径为r′,高为h′,根据三角形相似找出h′与r′的关系,然后表示出内接圆柱侧面积,最后利用基本不等式求出最值即可,注意等号成立的条件.
解答:
解:(1)设圆锥的底面半径为r,弧长为l,
∵圆锥的体积是12πcm3,其侧面展开图是中心角为216°的扇形,
∴
πr2
=12π…①,
=216×
…②,
解①②可得:r=3,l=5,圆锥的高为4,
圆锥侧面积:πrl=15π.(cm2).
(2)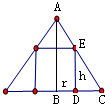 设内接圆柱的底面半径为r′,高为h′,如右图,
设内接圆柱的底面半径为r′,高为h′,如右图,
∵△CAB∽△CED,
∴
=
,即
=
,则h′=
(3-r′),
∴内接圆柱侧面积S=2πr′h′=2πr′×
(3-r′)=
r′(3-r′)≤
(
)2=6π,
当且仅当r′=3-r′,即r′=
时取等号,
∴内接圆柱侧面积最大值是6π.
∵圆锥的体积是12πcm3,其侧面展开图是中心角为216°的扇形,
∴
| 1 |
| 3 |
| l2-r2 |
| 2πr |
| l |
| π |
| 180 |
解①②可得:r=3,l=5,圆锥的高为4,
圆锥侧面积:πrl=15π.(cm2).
(2)
 设内接圆柱的底面半径为r′,高为h′,如右图,
设内接圆柱的底面半径为r′,高为h′,如右图,∵△CAB∽△CED,
∴
| ED |
| AB |
| CD |
| CB |
| h′ |
| 4 |
| 3-r′ |
| 3 |
| 4 |
| 3 |
∴内接圆柱侧面积S=2πr′h′=2πr′×
| 4 |
| 3 |
| 8π |
| 3 |
| 8π |
| 3 |
| r′+3-r′ |
| 2 |
当且仅当r′=3-r′,即r′=
| 3 |
| 2 |
∴内接圆柱侧面积最大值是6π.
点评:本题主要考查了圆锥的内接圆柱的侧面积,以及基本不等式在最值中的应用,同时考查了分析问题的能力,属于中档题.

练习册系列答案
相关题目
已知复数a+bi=
(a、b∈R),则z=b+(a-1)i在复平面上对应的点位于( )
| 2+i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
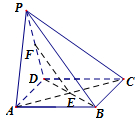 如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F.
如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F.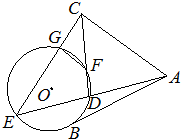 如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.