题目内容
数列{an}、{bn}的每一项都是正数,a1=8,b1=16,且an、bn、an+1成等差数列,bn、an+1、bn+1成等比数列,n=1,2,3,…
(Ⅰ)求a2、b2的值;
(Ⅱ)求数列{an}、{bn}的通项公式;
(Ⅲ)记
=
+
,证明:对一切正整数n,有
+
+
+…+
<
.
(Ⅰ)求a2、b2的值;
(Ⅱ)求数列{an}、{bn}的通项公式;
(Ⅲ)记
| 1 |
| cn |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| c1 |
| 1 |
| c2 |
| 1 |
| c3 |
| 1 |
| cn |
| 3 |
| 8 |
考点:数列与不等式的综合,等差数列的性质,等比数列的性质
专题:等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ)由an、bn、an+1成等差数列可得a2=2b1-a1=24.由bn、an+1、bn+1成等比数列可得
=b1b2,代入已知条件得到a2、b2的值;
(Ⅱ)由an、bn、an+1成等差数列,bn、an+1、bn+1成等比数列,得到2bn=an+an+1,an+1=
.联立得到2
=
+
,由此可知数列{
}是等差数列,由等差数列的通项公式求得bn,进一步得到an;
(Ⅲ)把数列{an}的通项公式代入
=
+
,整理后利用裂项相消法求其和,最后放缩得答案.
| a | 2 2 |
(Ⅱ)由an、bn、an+1成等差数列,bn、an+1、bn+1成等比数列,得到2bn=an+an+1,an+1=
| bnbn+1 |
| bn |
| bn-1 |
| bn+1 |
| bn |
(Ⅲ)把数列{an}的通项公式代入
| 1 |
| cn |
| 1 |
| an |
| 1 |
| an+1 |
解答:
解:(Ⅰ)由an、bn、an+1成等差数列,得2b1=a1+a2,
又a1=8,b1=16,
可得a2=2b1-a1=24.
由bn、an+1、bn+1成等比数列,
得
=b1b2,可得b2=
=36;
(Ⅱ)解:∵an、bn、an+1成等差数列,
∴2bn=an+an+1…①.
∵bn、an+1、bn+1成等比数列,
∴
=bnbn+1,
∵数列{an}、{bn}的每一项都是正数,
∴an+1=
…②.
于是当n≥2时,an=
…③.
将②、③代入①式,可得2
=
+
,
因此数列{
}是首项为4,公差为2的等差数列,
∴
=
+(n-1)d=2n+2,于是bn=4(n+1)2.
则an=
=
=4n(n+1).
当n=1时,a1=8,满足该式子,
∴对一切正整数n,都有an=4n(n+1);
(Ⅲ)证明:∵
=
=
(
-
),
∴
=
+
=
(
-
).
于是
+
+
+…+
=
[(1-
)+(
-
)+…+(
-
)+(
-
)]
=
(1+
-
-
)<
.
又a1=8,b1=16,
可得a2=2b1-a1=24.
由bn、an+1、bn+1成等比数列,
得
| a | 2 2 |
| ||
| b1 |
(Ⅱ)解:∵an、bn、an+1成等差数列,
∴2bn=an+an+1…①.
∵bn、an+1、bn+1成等比数列,
∴
| a | 2 n+1 |
∵数列{an}、{bn}的每一项都是正数,
∴an+1=
| bnbn+1 |
于是当n≥2时,an=
| bn-1bn |
将②、③代入①式,可得2
| bn |
| bn-1 |
| bn+1 |
因此数列{
| bn |
∴
| bn |
| b1 |
则an=
| bn-1bn |
| 4n2•4(n+1)2 |
当n=1时,a1=8,满足该式子,
∴对一切正整数n,都有an=4n(n+1);
(Ⅲ)证明:∵
| 1 |
| an |
| 1 |
| 4n2+4n |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| cn |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+2 |
于是
| 1 |
| c1 |
| 1 |
| c2 |
| 1 |
| c3 |
| 1 |
| cn |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 8 |
点评:本题考查等差数列和等比数列的性质,考查了等差数列和等比数列通项公式的求法,训练了裂项相消法求数列的和,训练了放缩法证明不等式,属难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
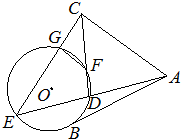 如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.