题目内容
已知x＞0，y＞0，a=x+y，b=
，c=λ
，若a，b，c能作为三角形的三边长，则正实数λ的范围是 ．
| x2-xy+y2 |
| xy |
考点：不等式比较大小
专题：不等式的解法及应用
分析：利用三角形任意两边之和大于第三边即可得出．
解答：
解：∵x＞0，y＞0，a=x+y，b=
，
∴a2-b2=3xy＞0，
∴a＞b．
∵a，b，c能作为三角形的三边长，
∴b+c＞a且a+b＞c，
即
+λ
＞x+y，x+y+
＞λ
．
由x+y+
＞λ
，
可得左边≥2
+
=3
，
∴λ＜3．
由
+λ
＞x+y，
∴λ＞
=
，
∵x+y+
≥3
，
∴λ＞1．
综上可得：1＜λ＜3．
故答案为：1＜λ＜3．
| x2-xy+y2 |
∴a2-b2=3xy＞0，
∴a＞b．
∵a，b，c能作为三角形的三边长，
∴b+c＞a且a+b＞c，
即
| x2-xy+y2 |
| xy |
| x2-xy+y2 |
| xy |
由x+y+
| x2-xy+y2 |
| xy |
可得左边≥2
| xy |
| xy |
| xy |
∴λ＜3．
由
| x2-xy+y2 |
| xy |
∴λ＞
x+y-
| ||
|
3
| ||
x+y+
|
∵x+y+
| x2-xy+y2 |
| xy |
∴λ＞1．
综上可得：1＜λ＜3．
故答案为：1＜λ＜3．
点评：本题考查了三角形任意两边之和大于第三边、不等式的解法、分母有理化，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
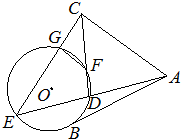如图，AB是⊙O的一条切线，切点为B，ADE、CFD都是⊙O的割线，AC=AB，CE交⊙O于点G．
如图，AB是圆O的直径，延长AB至C，使AB=2BC，且BC=2，CD是圆O的切线，切点为D，连接AD，则CD=