题目内容
已知定义域为R的函数f(x)=
是奇函数.
(1)求a的值;
(2)用定义证明f(x)在(-∞,+∞)上为减函数.
(3)若对于任意t∈R,不等式f(t2-2t)+f(k-2t2)>0恒成立,求k的范围.
| a-2x |
| 2x+1 |
(1)求a的值;
(2)用定义证明f(x)在(-∞,+∞)上为减函数.
(3)若对于任意t∈R,不等式f(t2-2t)+f(k-2t2)>0恒成立,求k的范围.
考点:函数恒成立问题,函数单调性的判断与证明,函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据函数是奇函数,建立条件关系即可求a的值;
(2)用定义证明f(x)在(-∞,+∞)上为减函数.
(3)根据函数的奇偶性和单调性之间的关系,将不等式不等式f(t2-2t)+f(k-2t2)>0进行转化即可,求k的范围.
(2)用定义证明f(x)在(-∞,+∞)上为减函数.
(3)根据函数的奇偶性和单调性之间的关系,将不等式不等式f(t2-2t)+f(k-2t2)>0进行转化即可,求k的范围.
解答:
解:(1)∵定义域为R的函数f(x)=
是奇函数.
∴f(0)=0,即f(0)=
=0,解得a=1,
即f(x)=
.
(2)任取x1,x2∈R,且x1<x2,
则f(x1)-f(x2)=
-
=
,
∵x1<x2,
∴2x1<2x2,即2x2-2x1>0,
即f(x1)-f(x2)=
>0,
f(x1)>f(x2),
即f(x)在(-∞,+∞)上为减函数.
(3)∵f(x)是奇函数,
∴不等式f(t2-2t)+f(k-2t2)>0恒成立等价为f(t2-2t)>-f(k-2t2)=f(2t2-k)恒成立,
∵f(x)在(-∞,+∞)上为减函数.
∴t2-2t<2t2-k,
即k<t2+2t,
∵t2+2t=(t+1)2-1≥-1,
∴k<-1.
| a-2x |
| 2x+1 |
∴f(0)=0,即f(0)=
| a-1 |
| 2 |
即f(x)=
| 1-2x |
| 2x+1 |
(2)任取x1,x2∈R,且x1<x2,
则f(x1)-f(x2)=
| 1-2x1 |
| 2x1+1 |
| 1-2x2 |
| 2x2+1 |
| 2(2x2-2x1) |
| (2x1+1)(2x2+1) |
∵x1<x2,
∴2x1<2x2,即2x2-2x1>0,
即f(x1)-f(x2)=
| 2(2x2-2x1) |
| (2x1+1)(2x2+1) |
f(x1)>f(x2),
即f(x)在(-∞,+∞)上为减函数.
(3)∵f(x)是奇函数,
∴不等式f(t2-2t)+f(k-2t2)>0恒成立等价为f(t2-2t)>-f(k-2t2)=f(2t2-k)恒成立,
∵f(x)在(-∞,+∞)上为减函数.
∴t2-2t<2t2-k,
即k<t2+2t,
∵t2+2t=(t+1)2-1≥-1,
∴k<-1.
点评:本题主要考查函数奇偶性的应用以及函数单调性的证明,利用函数的性质将不等式进行转化是解决本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
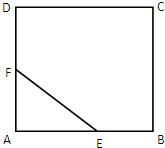 如图,有一块正方形区域ABCD,现在要划出一个直角三角形AEF区域进行绿化,满足:EF=1米,设角AEF=θ,θ∈[
如图,有一块正方形区域ABCD,现在要划出一个直角三角形AEF区域进行绿化,满足:EF=1米,设角AEF=θ,θ∈[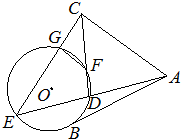 如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G. 如图,AB是圆O的直径,延长AB至C,使AB=2BC,且BC=2,CD是圆O的切线,切点为D,连接AD,则CD=
如图,AB是圆O的直径,延长AB至C,使AB=2BC,且BC=2,CD是圆O的切线,切点为D,连接AD,则CD=