题目内容
已知全集U=R，若集合A={x|3≤x＜10}，B={x|2＜x≤8}．
（1）求A∩B，A∪B，（∁UA）∩（∁UB）；
（2）若集合C={x|x＜a}，A⊆C，求a的取值范围．（结果用区间或集合表示）
（1）求A∩B，A∪B，（∁UA）∩（∁UB）；
（2）若集合C={x|x＜a}，A⊆C，求a的取值范围．（结果用区间或集合表示）
考点：集合的包含关系判断及应用,交、并、补集的混合运算
专题：集合
分析：（1）先按交与并的定义运算，然后转化（∁UA）∩（∁UB）=∁U（A∪B）求解，（2）利用数轴表示集合A，然后表示集合C满足C={x|x＜a}，A⊆C，数形结合求a的范围．
解答：
解；有题意A={x|3≤x＜10}，B={x|2＜x≤8}，得
（1）A∩B={x|3≤x＜10}∩{x|2＜x≤8}=[3，8]，
A∪B={x|3≤x＜10}∪{x|2＜x≤8}=（2，10），
又全集U=R，
则（∁UA）∩（∁UB）=∁U（A∪B）=（-∞，2]∪[10，+∞）；
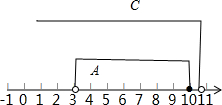
（2）A={x|3≤x＜10}，C={x|x＜a}，A⊆C，在数轴上表示为
则a≥10，所以a的取值范围是{a|a≥10}．
解；有题意A={x|3≤x＜10}，B={x|2＜x≤8}，得（1）A∩B={x|3≤x＜10}∩{x|2＜x≤8}=[3，8]，
A∪B={x|3≤x＜10}∪{x|2＜x≤8}=（2，10），
又全集U=R，
则（∁UA）∩（∁UB）=∁U（A∪B）=（-∞，2]∪[10，+∞）；
（2）A={x|3≤x＜10}，C={x|x＜a}，A⊆C，在数轴上表示为
则a≥10，所以a的取值范围是{a|a≥10}．
点评：本题考查集合的运算解题技巧是熟练掌握交并补的定义，还要学会使用数轴数形结合解题．
练习册系列答案
阅读快车系列答案
相关题目
设集合U={1，2，3，4，5}，A={1，2，3}，B={2，5}，则（∁UA）∩（∁UB）=（ ）
| A、{2} | B、{2，3} |
| C、{4} | D、{1，3} |
如图，正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2，D是BC的中点．